RF 001 - Eigenmode ports and S-parameters

Model definition

A 3D microstrip track aligned with the x-axis is considered. The corresponding 2D cross-section is illustrated below.

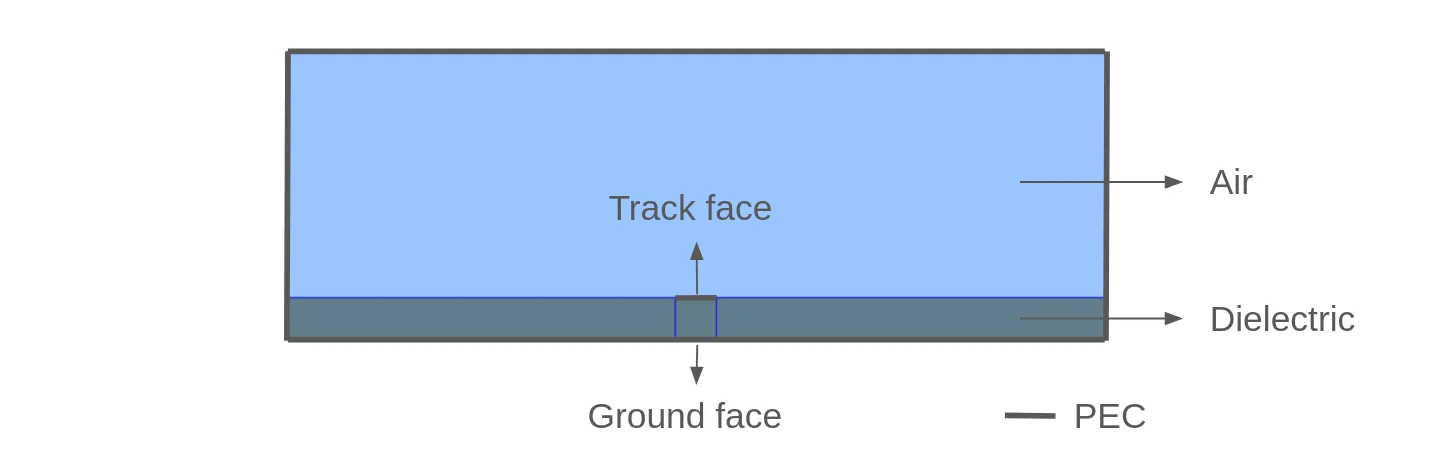
Component	XYZ dimensions [mm]	Center Z elevation [mm]
Air box	10 x 10 x 3	0.5/2 + 3/2
Track box	10 x 0.5 x 0.5	0
Dielectric box	10 x 10 x 0.5	0

The relative electric permittivity of the dielectric is set to 10 and the working frequency ranges from 5 GHz to 15 GHz.

Use the built-in CAD tools to draw the three boxes in the microstrip stack. The track is modeled as a perfect conductor and its thickness is neglected. A box is drawn below the track to create a CAD surface for the track at the dielectric-air interface.
An alternative setup of the geometry is to provide your .step or .gds file.
Klayout is a popular free tool in the semiconductor industry to easily create a .gds file for the above geometry.

---

Simulation setup guide

Here, you’ll find a simplified guide on setting up this simulation in Quanscient Allsolve.

Step 1 - Create the geometry

In the geometry editor, draw three boxes as detailed above to ready the microstrip geometry.

Step 2 - Define regions, materials and shared expressions

Proceed to the properties editor to define the dielectric and air materials. Pick the Air material from the materials database and assign it to the corresponding CAD volume. Create a new material for the dielectric layer and add its permittivity, permeability and conductivity properties respectively to $10 \cdot \text{epsilon}0$, $\text{mu}0$ and $0$. The track material is not required here as it is modeled as a perfect conducting face.

For later use, also define a shared expression for the frequency. Name it freq and set it to a default 10e9 Hz. This expression can then be used throughout Allsolve, where applicable.

Step 3 - Define the physics and apply boundary conditions

Proceed to the physics editor and add the electromagnetic waves physics. In this physics, add interaction perfect conductor and assign it to the surfaces marked as PEC above.

Choosing the PEC boundaries

The PEC condition is here only strictly required on the track and ground faces. Adding it also on the other marked faces will not make a difference as long as the side and height extents of the dielectric and the air are large enough. For the sizes used here however it is beneficial to set all side faces to PEC as this will lead to magnetic field lines being tangential to the box boundary and thus will enforce that they close within the computational domain. Should the modeled device emit a non-negligible amount of waves, then perfectly matched layers (PMLs) or absorbing conditions (ABCs) must be used.

The eigenmode port interaction is now set up at both x-end faces.
Adding an eigenmode port interaction at a port has the following three effects:

• calculate the propagating modes patterns and their propagation constants
• drive the selected mode into the waveguide
• absorb all the power of the selected mode that is reflected back to the port

Eigenmode port location

The location should be at the boundary of the geometry to avoid any ambiguity in the material properties used for the mode calculation. This can happen when the port face is located at the interface between two different materials.

Eigenmode port face selection

For the eigenmode analysis to return the propagating modes with an accurate pattern and propagation constant it is necessary to provide a port face that covers all the area where the electric field and magnetic field intensity cannot be neglected. Failing to do so will lead to a higher level of mode insertion reflection since only an approximation of the actual propagating mode is fed into the waveguide. There is a downside however in providing large port faces to the eigenmode port: undesired modes might be found by the eigenmode solver, such as for example the classical TE and TM modes of a rectangular port.

Multimode waveguides

If more than one mode can propagate in the waveguide then a given eigenmode port will deal only with its target mode. This means that the power that arrives at a port is fully reflected back into the waveguide for all other modes. S-parameters calculated at a port also only measure the power in terms of the target mode. Adding one eigenmode port interaction for each propagating mode at a port will solve the issue by dealing separately with each mode: the individual power of each mode is then absorbed and no power is reflected back if all modes are accounted for. This mathematically holds because all modes returned by the eigenmode solver are orthogonal to each other.

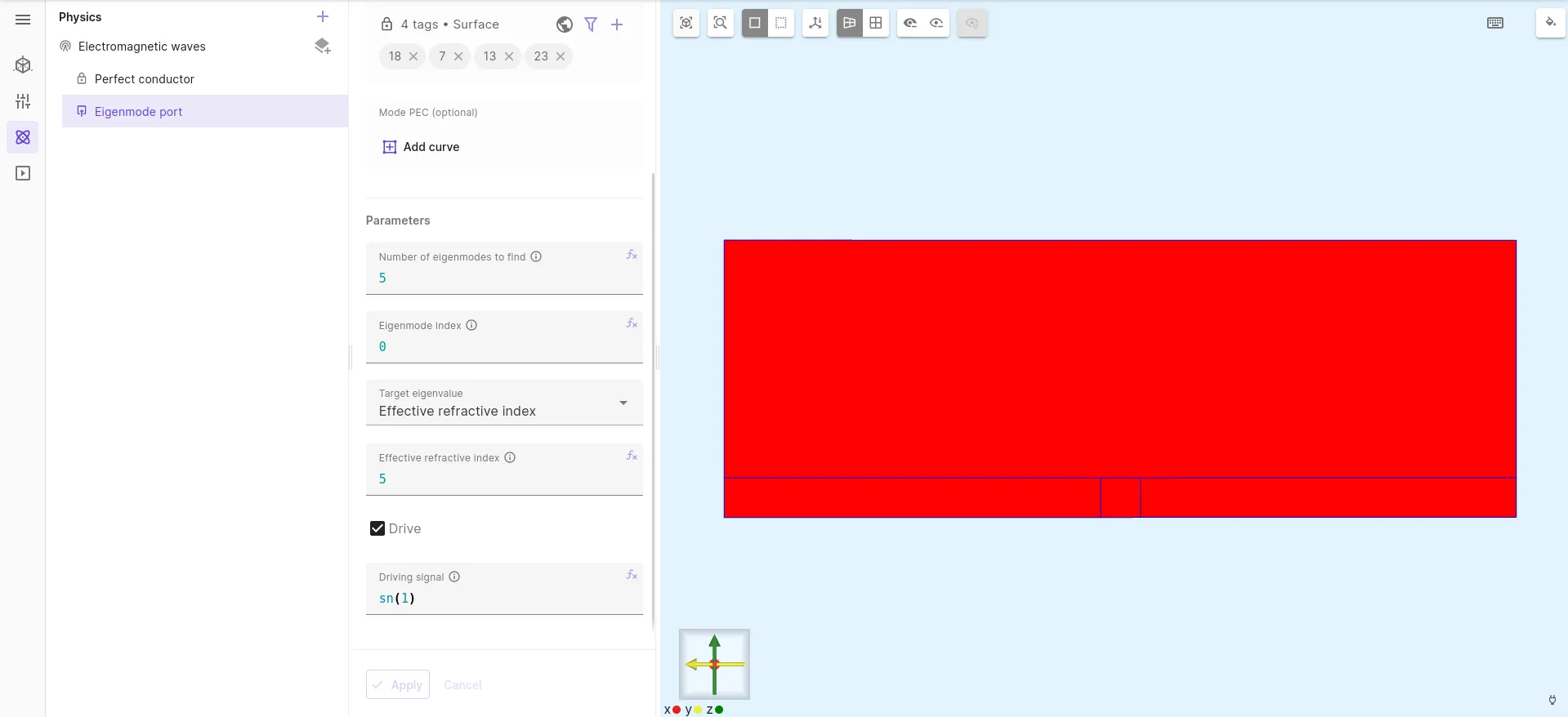
Two eigenmode port interactions should be setup as detailed in the above picture: one interaction per port face.

This type of port performs an eigenmode analysis to find the propagating modes and it can be tuned with the following options:

• the optional mode PEC region allows to enforce perfect electric conductor regions specifically for the mode calculation step, in addition to the ones that have been defined in the electromagnetic waves physics. This is of use, for example, for GCPWs with vias between the top and bottom ground conductors, when the vias are not touching the eigenmode port region: in such situations, the eigenmode solver cannot be aware of the electric contact between those grounds and some modes could be returned that do not enforce that the grounds are connected together
• the number of eigenmodes to find in the analysis phase can be specified (in this case it is left to the default since only one mode can propagate at the GHz frequencies of interest)
• the eigenmode index allows to choose which mode must be considered at the port out of all modes that have been found by the eigenmode solver. If several modes can propagate, then it is recommended to first run a port mode analysis at simulation time (see below) and come back to this section to select the index of the desired mode. In this case index 0 is selected as it is the first and only propagating mode
• the target eigenvalue can be selected to focus the eigenmode analysis around a propagation constant of interest. This can also be advantageously used to order the eigenmodes, starting from the eigenvalues closest to the target. For convenience one might select the effective refractive index target method: the number that must be provided there is between the relative permittivity of the air and the dielectric medium and is therefore easier to guess correctly without hand calculations
• the drive tick box determines which port is actively powered and which port is only listening and not powered. This option only affects the output electric field profile. It does not affect the S-parameter calculation as the powering for this analysis is determined by Allsolve by powering each port individually one after the other
• the product of the driving signal and the selected magnetic field mode is what is fed into the waveguide. The driving signal can be used to set the port reference phase such as needed for example to drive phased-array antennas. The argument expression can be provided explicitly such as $\text{sin}(2\pi\cdot 1e9 \cdot t+\pi/2)$ or using shared expressions such as $\text{sin}(2\pi\cdot \text{freq} \cdot t+\pi/2)$. A shortcut sn(1) or cn(1) can be used respectively as an alias for $\text{sin}(2\pi\text{f}\text{t})$ and $\text{cos}(2\pi\text{f}\text{t})$ where the frequency will be provided at simulation time for a harmonic analysis type. The input power for a phase shifted sine or cosine wave of peak amplitude 1 is 1W time-averaged

Step 4 - Set up the simulation run

Proceed to the Simulations editor and add a new simulation. Add a new mesh that suits your requirements of accuracy.

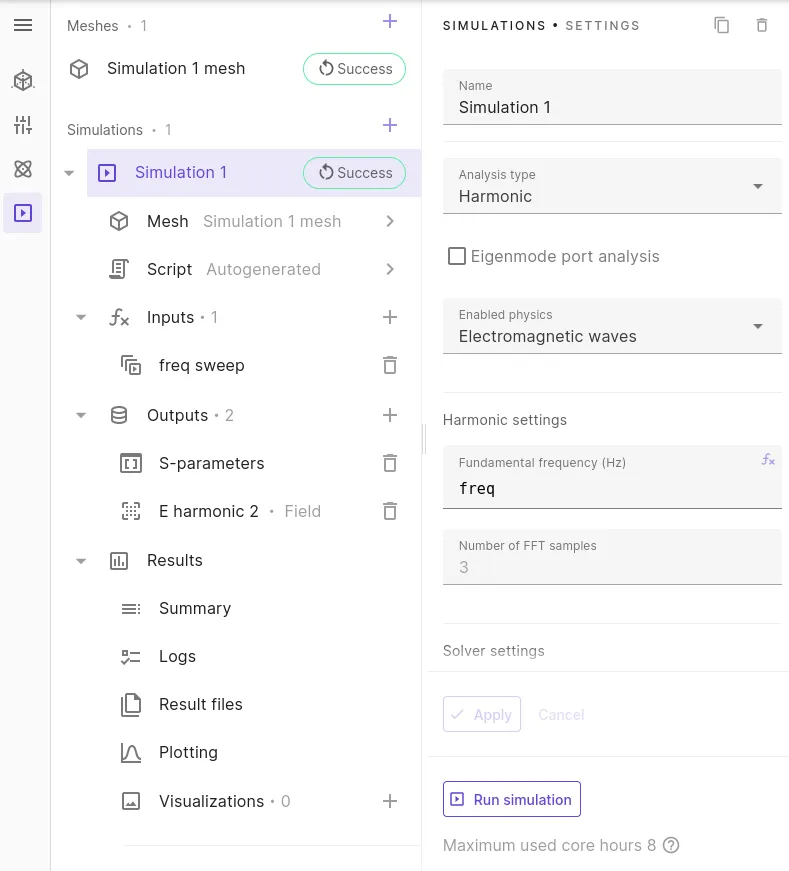
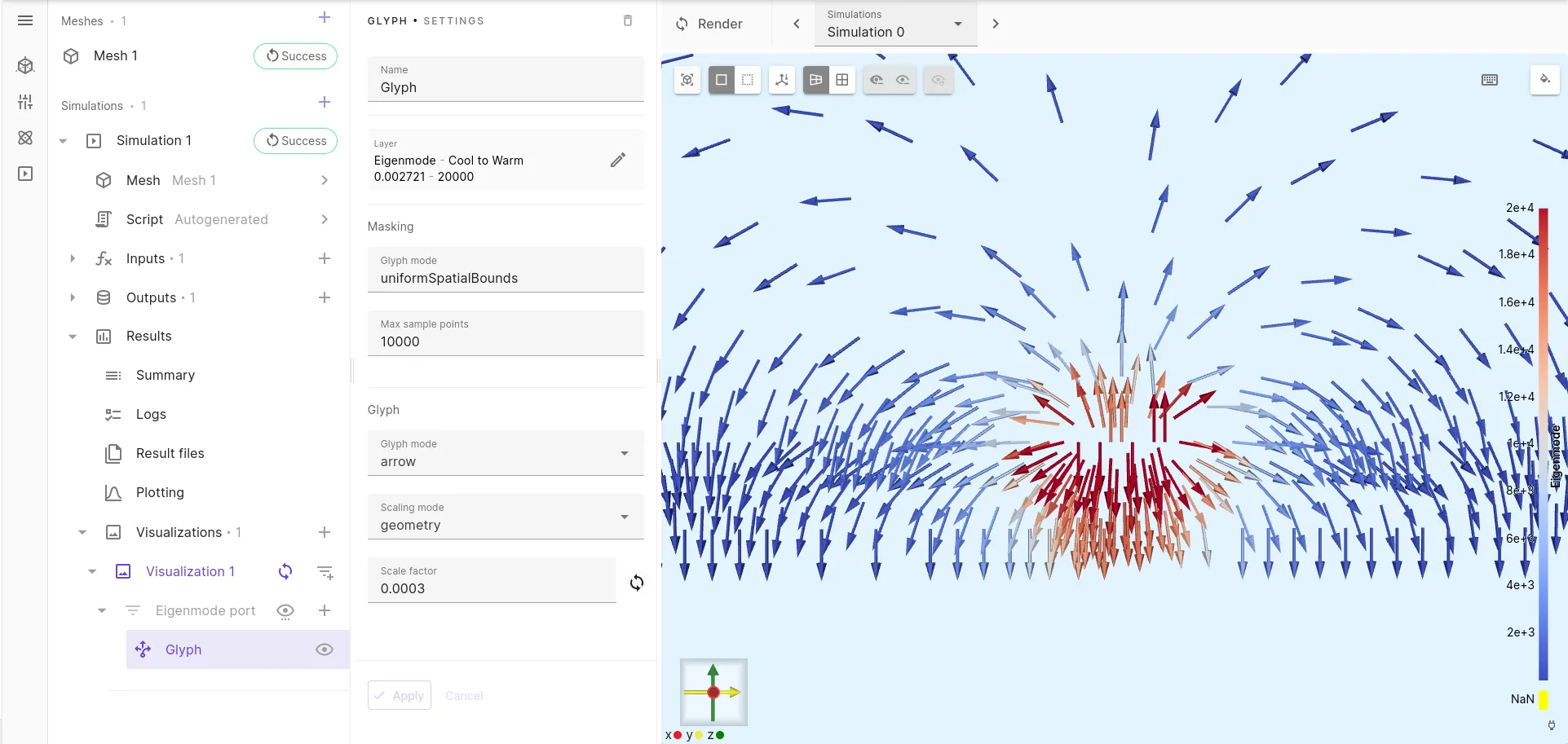
Set up the simulation as detailed in the picture above. The analysis type is harmonic, so that the steady-state solution at a given frequency is obtained. For multimode waveguides, tick the eigenmode port analysis box, then run the simulation and visualize each propagating mode pattern using the glyph filter as illustrated below, or check the log output to get more info regarding the modes found such as the propagation constant and the effective refractive index. Once the desired mode index has been identified, go back to the eigenmode port interaction setup to select the corresponding index (use 0 for the first mode in the list). Don’t forget to untick the eigenmode port analysis before the next run.
In this case, a GHz range driving frequency is used and only a single QTEM mode can propagate, hence the above mode analysis step is not required.

Select as output at least the S-parameters. If you want to visualize the profile of the real part/imaginary part (that is, the harmonic 2/3) of the electric field solution, also add the E field output on the region of interest.

Rendering performance

Tick the skin only box to save the output field only on the skin of the selected volume if the whole volumetric data is not of interest.

To perform a frequency sweep from 5 GHz to 15 GHz by steps of 1 GHz, add the sweep input linspace(5e9, 15e9, 11).

Mode crossings for multimode waveguides

When performing a frequency sweep or other types of sweeps, make sure the desired mode is the one used at eigenmode ports. For modes with propagation constant or effective refractive index changing with frequency, the ordering of the modes returned by the eigenmode solver might change with frequency. New modes might also be returned as the frequency is increased in the sweep. The mode actually used at every eigenmode port is available to visualize after the simulation has run.

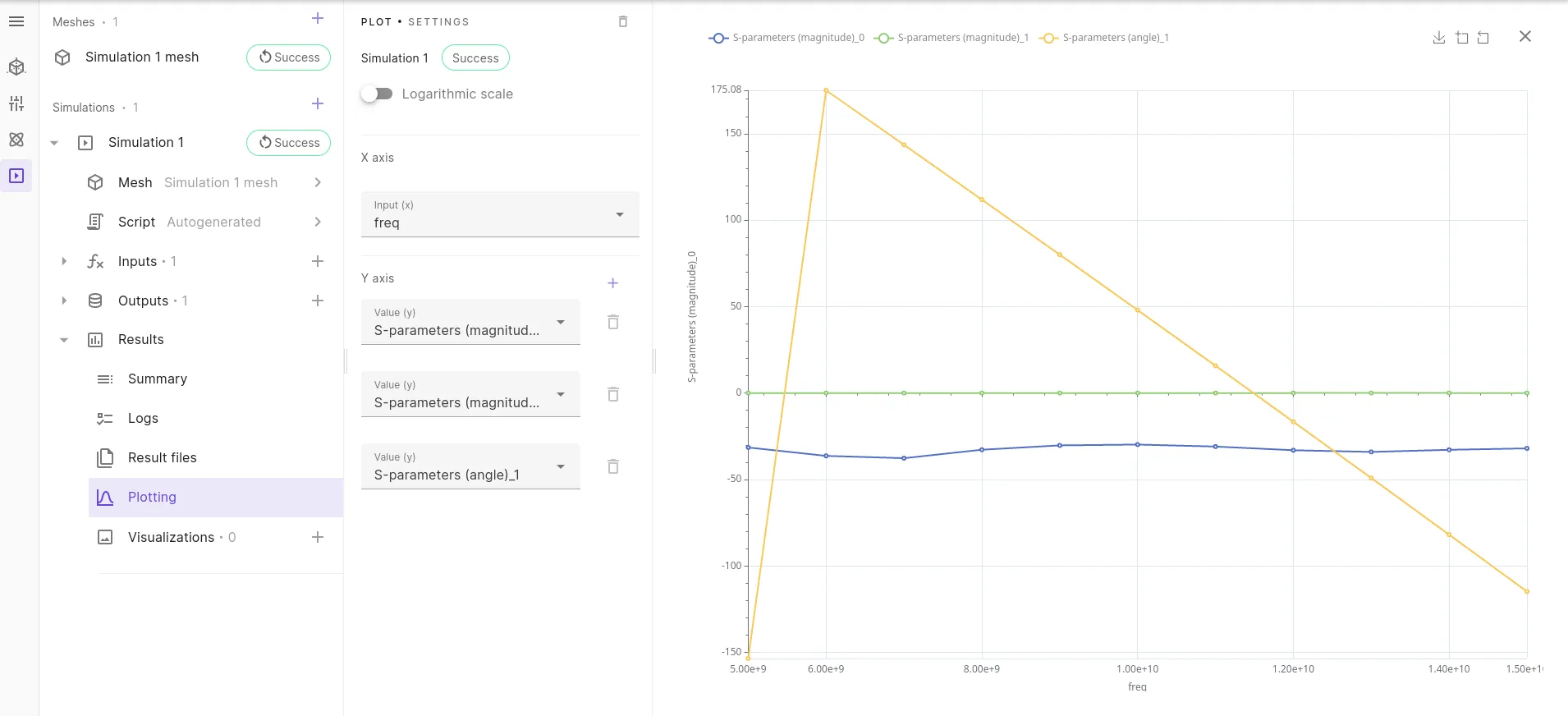
Run the simulation, then go to the plotting option and select for example the S12 angle output to show the microstrip line delay sweep versus frequency illustrated on the picture below. If the simulation is set up properly you should obtain a very low S11 magnitude (in dB) and a close to 0 dB S12 magnitude. The values will get closer to the exact S11 and S12 values as the mesh is refined.