Bending of a cantilever beam

In this tutorial, the bending of a cantilever beam is simulated.

A cantilever is a rigid structure that extends horizontally and is unsupported at one end ¹. It is widely used in construction and serves as a baseline simulation for structural mechanics.

Model definition

The model comprises a small aluminium beam built from a single box element. The beam is clamped from one of its end surfaces, and extends horizontally like a flagpole attached to a wall.

A load is evenly applied to the top surface of the beam, bending it downwards. The maximum Z-displacement is solved during simulation.

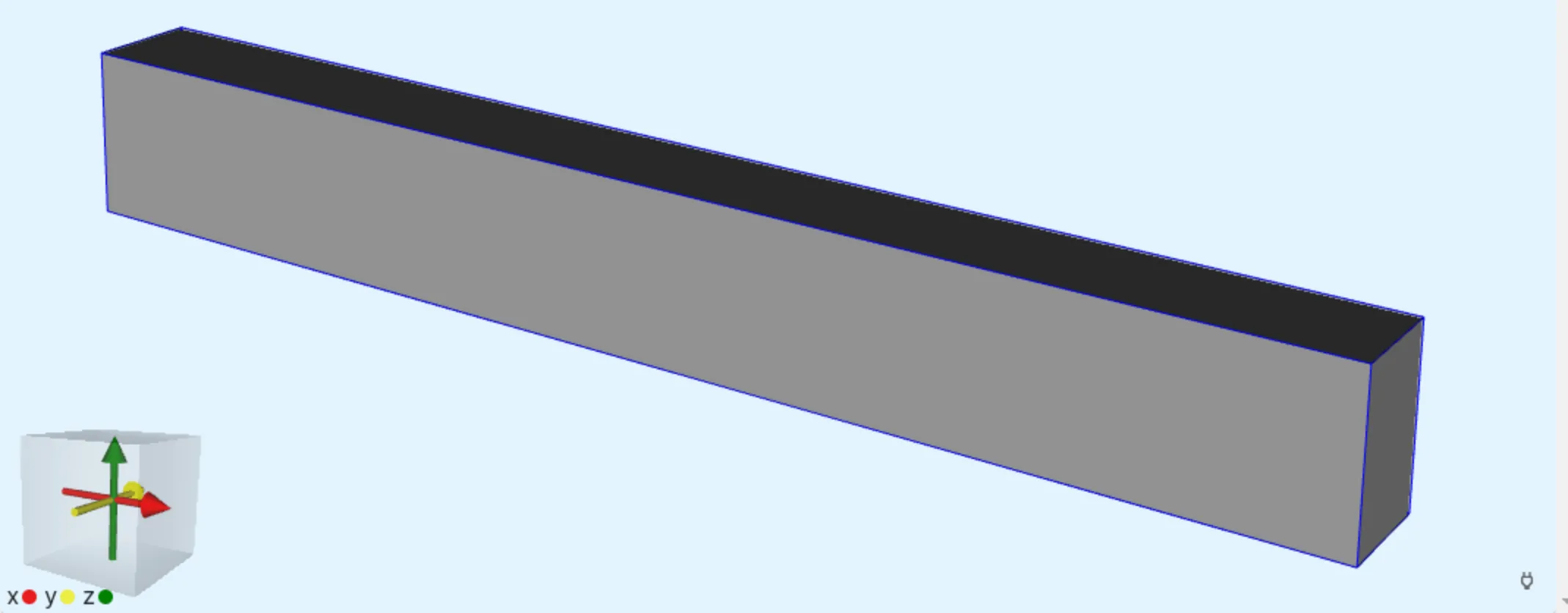
Model geometry

Name	Element type	XYZ dimensions [mm]
Cantilever beam	Box	24 x 2 x 3

Material Data

Aluminium

Property	Value
Poisson’s ratio	0.32
Young’s modulus [Pa]	68e9

Boundary conditions

Name	Type	Value [X, Y, Z]
left X-plane	Clamp	[0, 0, 0]
top Z-plane	Load [N]	[0, 0, -1000]

Output Results

Maximum Z-displacement.

Step-by-step guide

Below, you’ll find a detailed step-by-step tutorial on how to set up a cantilever beam simulation in Quanscient Allsolve.

Step 1 - Build the geometry

1. Start with a new project and name it Cantilever beam.

2. Start out with a box element. A 1 x 1 x 1 m box is built by default.

3. Edit the size of the box in settings:

   Name	Element type	Center point [m]	Size [m]	Rotation [deg]
   box	Box	X: 0	X: 24e-3	X: 0
   		Y: 0	Y: 2e-3	Y: 0
   		Z: 0	Z: 3e-3	Z: 0

4. Rebuild the box with correct dimensions.

5. Confirm model changes before moving on.

Step 2 - Define shared regions

1. Go to the Common sidebar.

2. Define shared regions:

   Name	Region type	Target
   clamp	Surface	X direction bottom surface (1)
   top	Surface	Z direction top surface (6)

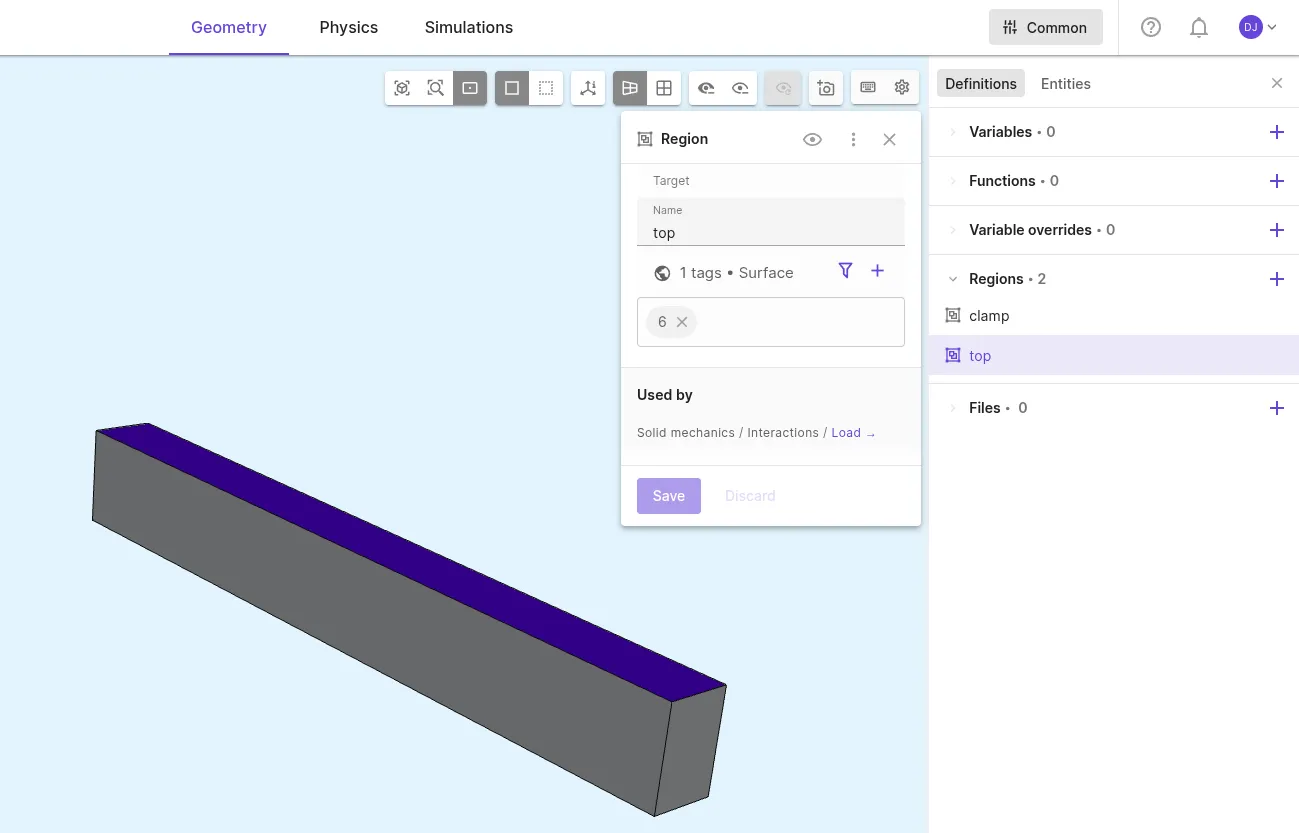
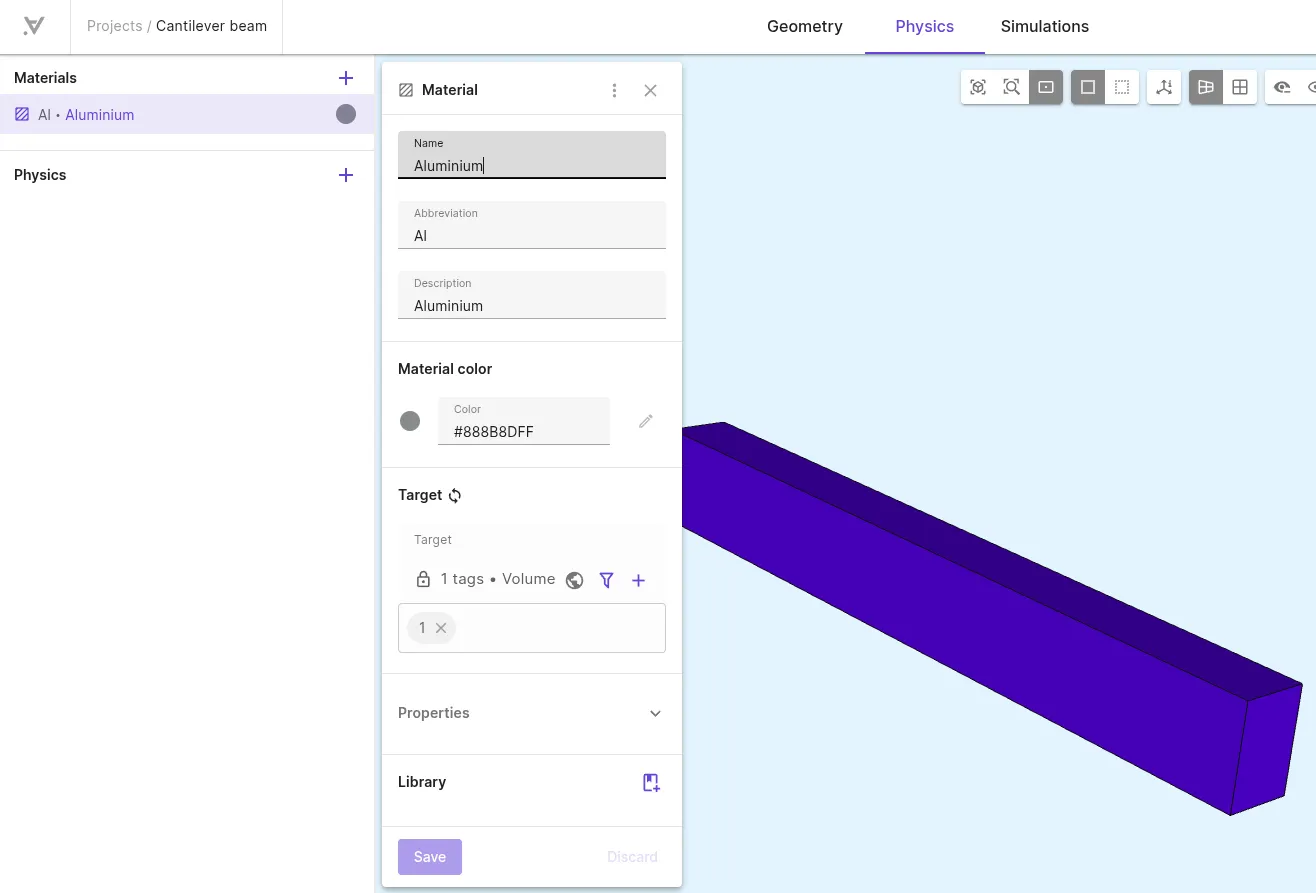
Step 3 - Define the material

Assign the predefined Aluminium material to the beam volume (1).

Step 4 - Define the physics & boundary conditions

1. Go to the Physics section.

2. Add the Solid mechanics physics.

   Not selecting a target for a physics makes it default to the whole model. Let solid mechanics target default to the beam volume.

   Physics	Target
   Solid mechanics	Beam (volume 1)

3. Add a Clamp interaction to Solid mechanics.

   Name	Interaction type	Target
   Clamp	Clamp	clamp shared region (surface 1)

   This boundary condition will constraint all components of the displacement vector in the targeted region to zero displacement: $u_x = 0$, $u_y = 0$, $u_z = 0$.

4. Add a Load interaction to Solid mechanics.

   Name	Interaction type	Target	Value [X; Y; Z]
   Load	Load	top shared region (surface 6)	[0; 0; -1000]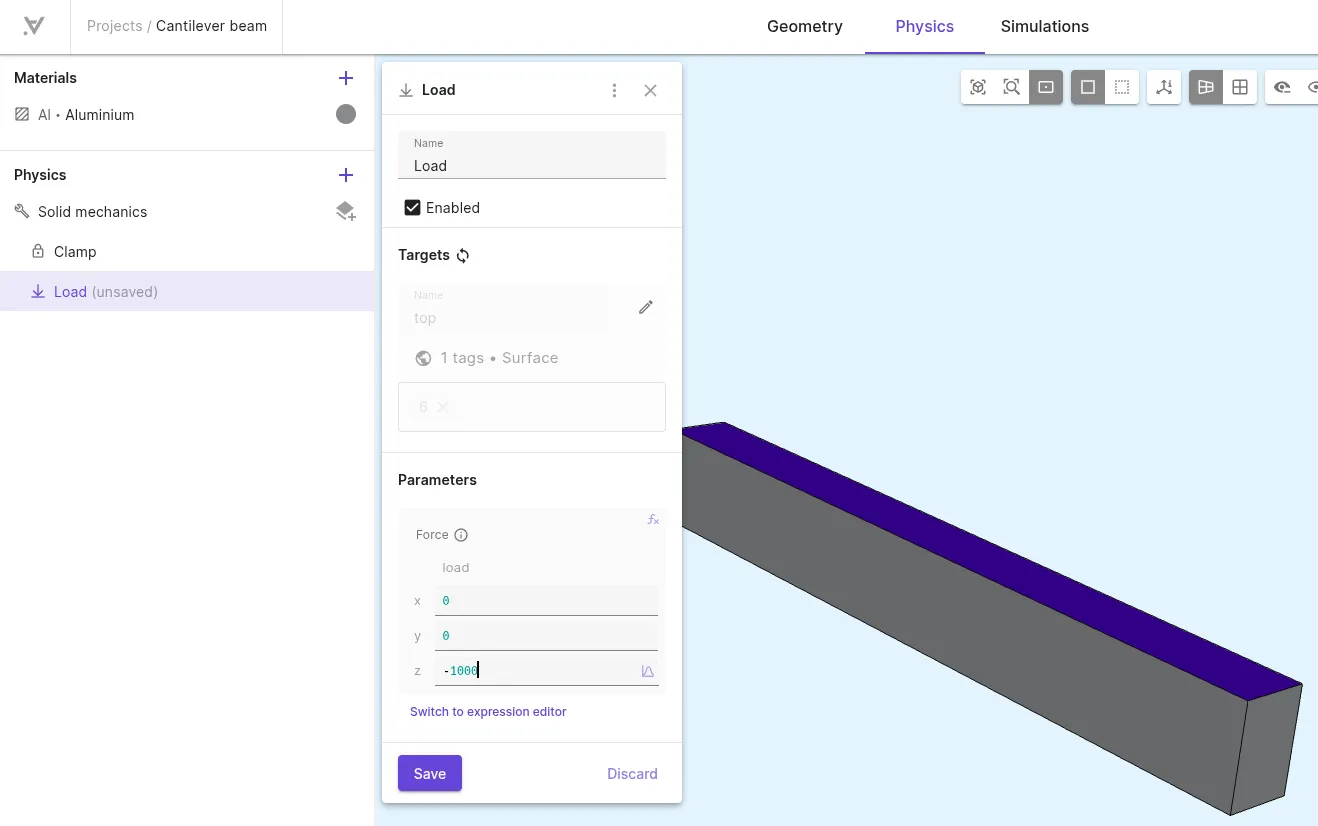

   

Step 5 - Generate the mesh

1. Proceed to the Simulations section.

2. Generate a new mesh with default settings and check the preview.

Step 6 - Apply simulation settings & run

1. Create a new simulation.

2. Set Analysis Type to Steady state.

3. Select the mesh you generated as the mesh for your simulation.

4. Add the displacement field output u.

5. Run the simulation.

Step 7 - Visualize results

1. Add a visualization for the u field.

2. Add Warp to the visualization and activate it.

3. Click on the Refresh icon next to Warp scale factor.

4. Render the deformed geometry scaled up according to the scale factor.

   

   

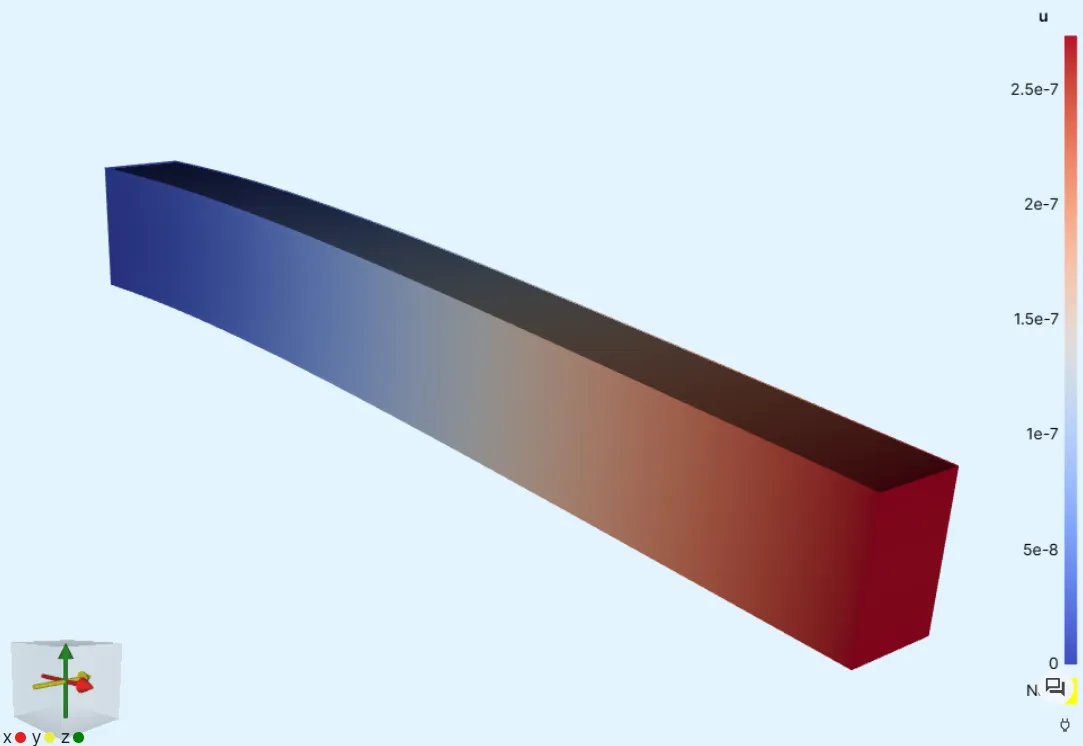
   Here, the scale factor is 8772.

References

Footnotes

1. https://en.wikipedia.org/wiki/Cantilever ↩