RF 002 - Lumped ports and RLC components

Prerequisites

This example uses the perfect conductor and eigenmode port interactions. These topics are covered in more detail in the documentation example RF 001.

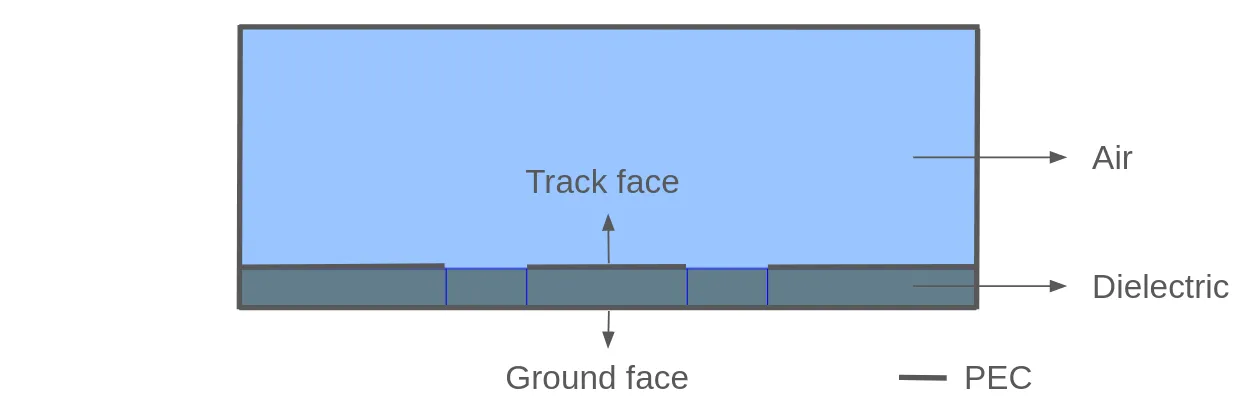
Model definition

A thin slice of a 3D grounded coplanar waveguide (GCPW) aligned with the x-axis is considered. The corresponding 2D cross-section is illustrated below.

Component	XYZ dimensions [mm]	Center Z elevation [mm]
Air box	0.5 x 10 x 3	0.5/2 + 3/2
Track box	0.5 x 2 x 0.5	0
Spacer box	0.5 x 4 x 0.5	0
Dielectric box	0.5 x 10 x 0.5	0

The relative electric permittivity of the dielectric is set to 5 and the drive frequency is 10 GHz.

Use the built-in CAD tools to draw the four boxes in the GCPW stack. The track and ground is modeled as a perfect conductor and its thickness is neglected. A box is drawn below the track to create a CAD surface for the track at the dielectric-air interface. Another box is drawn under the track and the spacer to create CAD surfaces for the grounds on the sides of the track. An alternative setup of the geometry is to provide your .step or .gds file.
Klayout is a popular free tool in the semiconductor industry to easily create a .gds file for the above geometry.

Simulation setup guide

Here, you’ll find a simplified guide on setting up this simulation in Quanscient Allsolve.

Step 1 - Create the geometry

In the Model section, draw four boxes as detailed above to ready the GCPW geometry.

Step 2 - Define regions, materials and shared expressions

Proceed to the Properties section to define the dielectric and air materials. Pick the Air material from the materials database and assign it to the corresponding CAD volume. Create a new material for the dielectric layer and add its permittivity, permeability and conductivity properties respectively to $5 \cdot \text{epsilon}0$, $\text{mu}0$ and $0$. The track and ground materials are not required here as they are modeled as perfect conducting faces.

For later use, also define a shared expression for the waveguide termination resistor. Name it R and set it to a default 50 Ohms. This expression can then be used throughout Allsolve, where applicable.

Step 3 - Define the physics and apply boundary conditions

Proceed to the Physics section and add the electromagnetic waves physics.

In this physics, add interaction perfect conductor and assign it to the surfaces marked as PEC above.

The eigenmode port interaction is now set up at the minimum x-end face. Since only a single mode can propagate at the frequency of interest, most default settings can be left as they are. Toggle the target eigenvalue to provide the effective refractive index value 5. The actual value for the QTEM that propagates is between the relative permittivity of the air and of the dielectric. Should an analysis frequency high enough be selected so that another type of mode can propagate, then the one with an effective refractive index closest to 5 will be returned first and selected if the default eigenmode index of 0 is used.

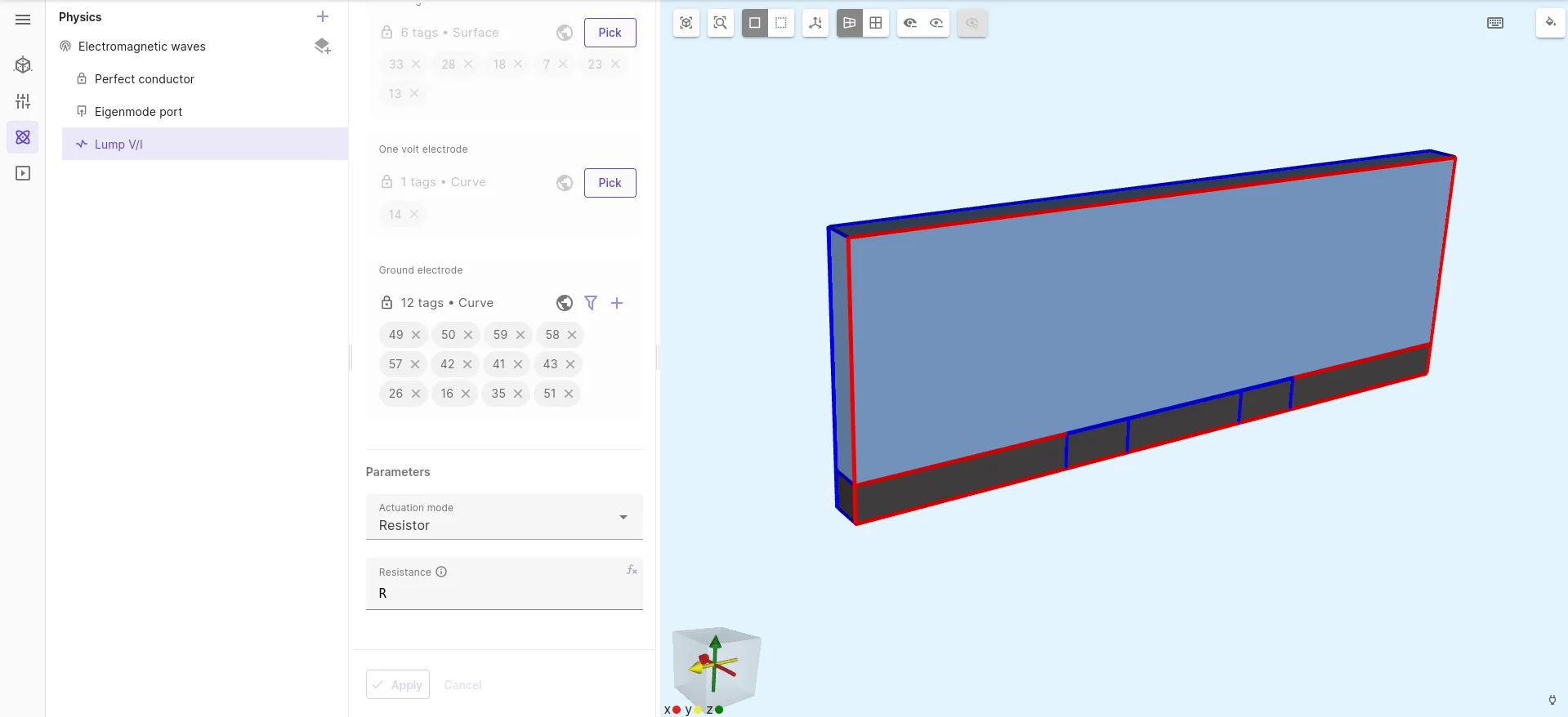
The other end face of the GCPW will in this example not be terminated with an eigenmode port. Instead the lumped port will be explored.

A lumped port works by forcing the tangential electric field at the port face to a profile provided by the user through an electrostatic resolution (user provided 1V and 0V regions are considered and the DC electric field profile between these two regions is computed). The voltage V at the 1V region is readily usable at a lumped port.

Working with voltages in RF

Mathematically speaking, the concept of electric potential only makes sense in DC. One will nevertheless get good agreement with reality as long as the electromagnetic wavelength in the material at the port is much larger than the port size.

The total current I is also readily usable at a lumped port without requiring any user input: it is equal to the current entering the waveguide at the 1V region, or minus the current entering the waveguide at the 0V region. In other words, if one considers the port face as being a current sheet, the current I is positive when it is opposite to the port electric field direction.

Lumped port current sheet excitation profile

The lumped port is excited through a tangential magnetic field profile that varies along the port face. This excitation can be compared to having at the port face a current sheet with a given current density profile. The current density profile at a lumped port face is entirely determined by the electromagnetic waves equations, given the desired electric field profile and track current. In practice, the current density profile is such that the propagating mode is excited, as this is the only way for current to flow in the track. For multimode waveguides there is no guarantee that the lumped port will not excite modes that do not match the target electric field profile. The latter will only favor the power flow through the corresponding mode but power will also flow through other modes, depending on the waveguide impedance for each mode.

The quantities V and I available at the port can be used to connect an RLC circuit at the lumped port or between two lumped ports. In this example, a lumped resistor is connected to the port using the easy to use resistor option, but alternatively the circuit coupling option could be used with equation $V + RI = 0$. Connecting an RL and RLC circuit with that option could be done respectively with equation $V + RI + L\frac{\partial I}{\partial t} = 0$ and $\frac{\partial V}{\partial t} + R\frac{\partial I}{\partial t} + L\frac{\partial^2 I}{\partial t^2} + I/C = 0$.

Lumped port location

The location can be either inside the electromagnetic waves physics region or at its boundary.

Differences between eigenmode ports and lumped ports

Lumped ports do not require an eigenmode analysis and are therefore restricted to mode profiles that can be accurately captured using an electrostatic resolution between two electrodes, such as the QTEM mode in this example. Furthermore, while the default power input by an eigenmode port is 1W time-averaged, the power fed into the waveguide by a lumped port is entirely determined by the user. Absorbing reflected power at a driving lumped port must also be handled by the user with a matching impedance ending.

The lumped port setup is illustrated below.

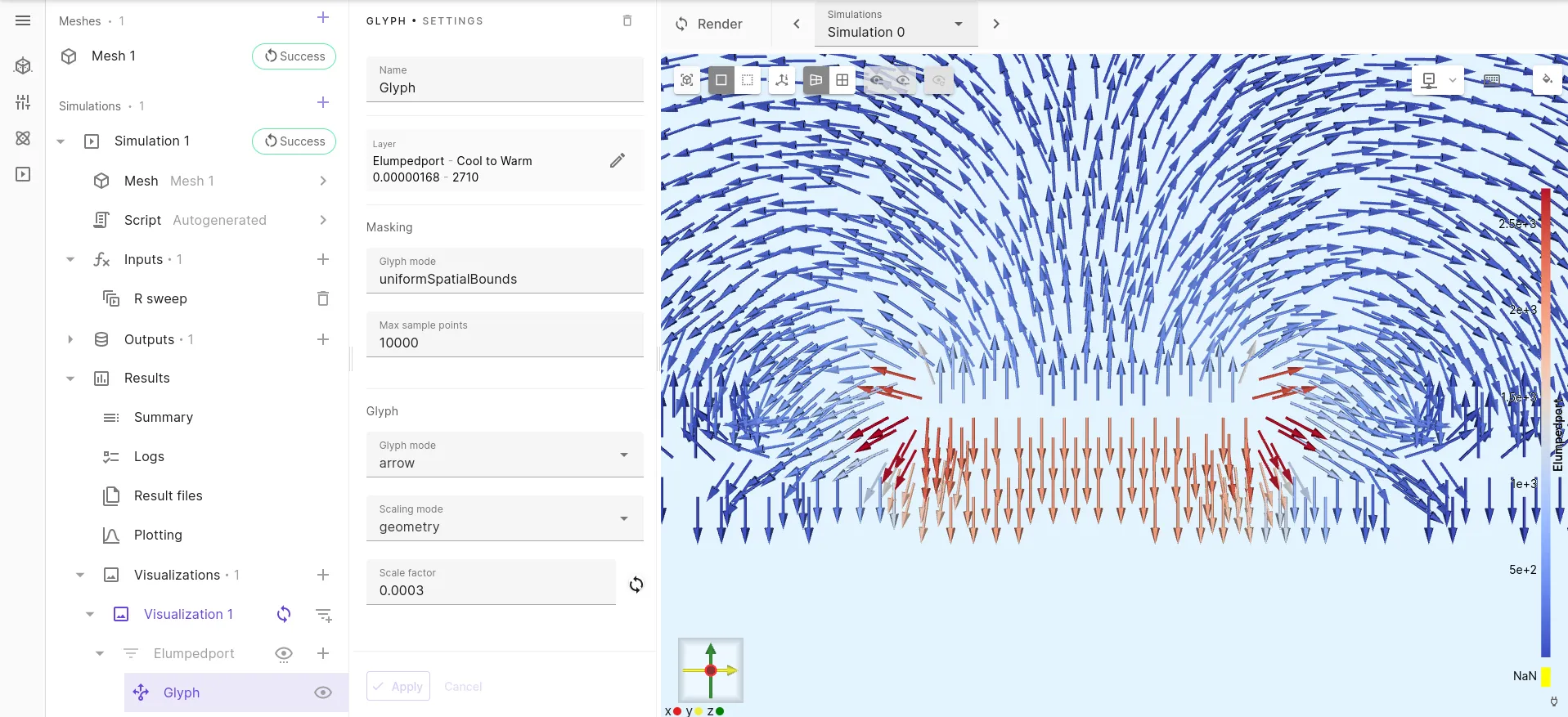
The mode profile at the lumped port for this GCPW is illustrated below.

Step 4 - Set up the simulation run

Proceed to the Simulations section and add a new simulation. Add a new mesh that suits your requirements of accuracy. Refining the mesh close to the track electrode and the spacer is beneficial for increased accuracy. This can be achieved by refining the track and spacer surfaces or the volumes below. Alternatively a structured mesh can be set up for these volumes to control the exact shape and density of the mesh.

Set up the simulation. The analysis type is harmonic, so that the steady-state solution at a given frequency is obtained. For multimode waveguides, tick the eigenmode port analysis box, then run the simulation and visualize each propagating mode pattern using the glyph filter similarly as shown above for the lumped port mode, or check the log output to get more info regarding the modes found such as the propagation constant and the effective refractive index. Once the desired mode index has been identified, go back to the eigenmode port interaction setup to select the corresponding index (use 0 for the first mode in the list). Don’t forget to untick the eigenmode port analysis before the next run.
In this case, a 10 GHz driving frequency is used and only a single QTEM mode can propagate, hence the above mode analysis step is not required.

Select as output at least the S-parameters. If you want to visualize the profile of the real part/imaginary part (that is, the harmonic 2/3) of the electric field solution, also add the E field output on the region of interest.

Rendering performance

Tick the skin only box to save the output field only on the skin of the selected volume if the whole volumetric data is not of interest.

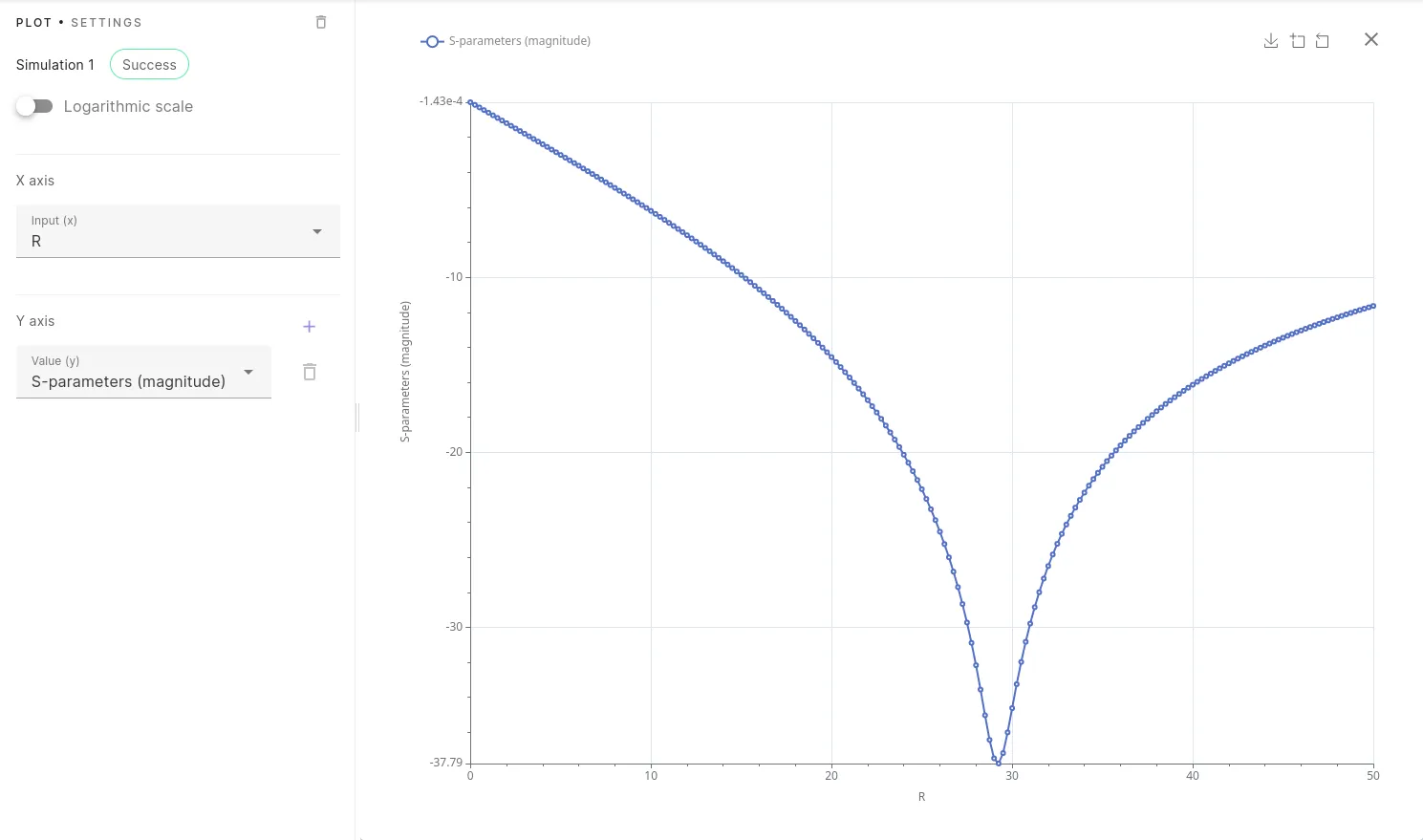
To perform a resistance load sweep from 0 Ohm to 50 Ohm by steps of 1 Ohm, add the sweep input linspace(0, 50, 51) as shown in the picture below. Depending on your plan, the simulations in the sweep will start by more or less large batches at the same time, running on separate hardware instances.

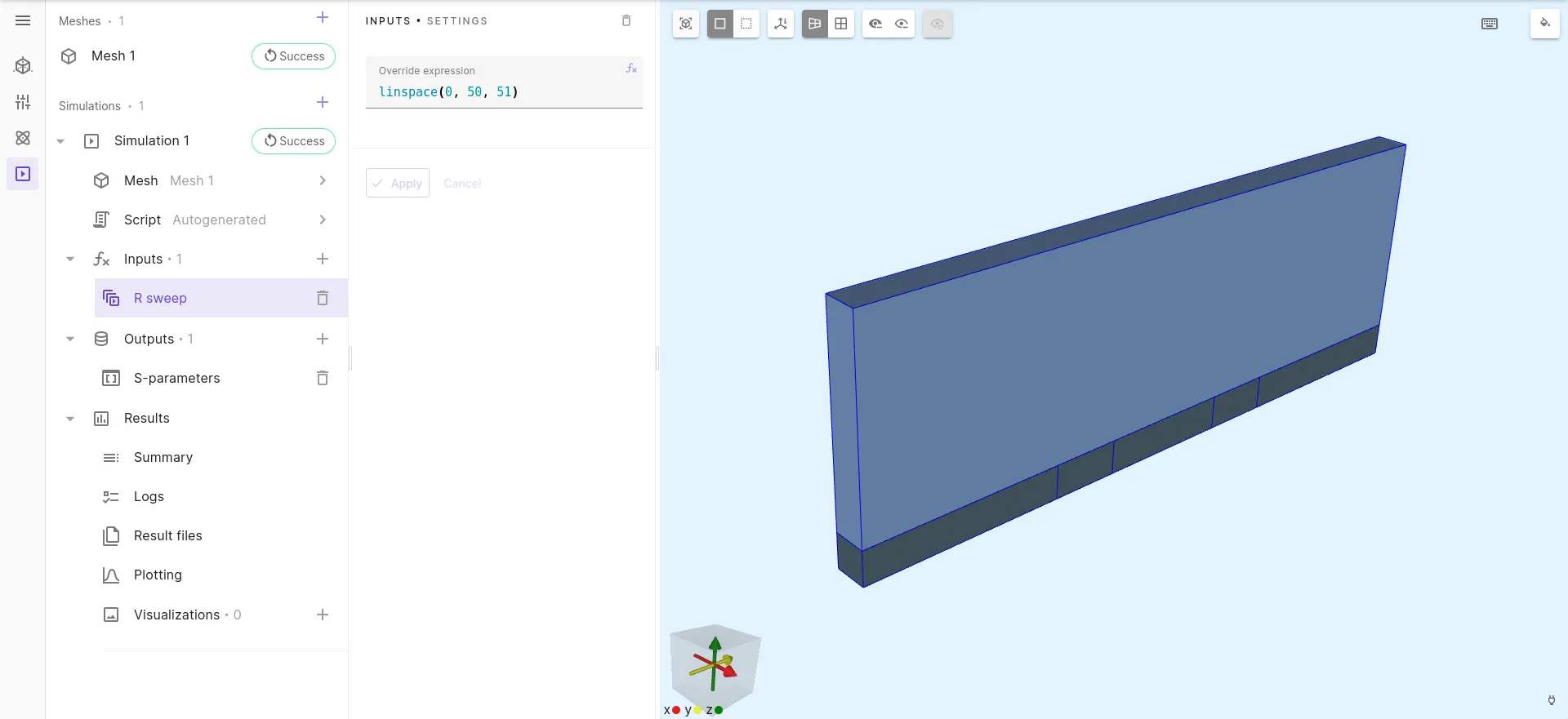
Run the simulation, then go to the plotting option and select the S11 magnitude in dB to show the amount of reflection created by the lumped port R load for various values of R.

The swept curve is shown below: it indicates that terminating the waveguide with a 29.25 Ohm resistor gives load matching with a very low -38 dB mode reflection coming back to the eigenmode port. This is as low as one would get with an eigenmode port used instead of the lumped port and it highlights the accuracy of the lumped port.

The value found matches the GCPW impedance value 29.13 Ohm obtained from usual online calculators.