Permanent magnet synchronous electric motor

In this tutorial, a 3D permanent magnet synchronous electric motor is considered under magnetostatic conditions using the φ-formulation.

Model definition

Instead of the whole motor, only a 1/8 slice of the motor is modeled. The 1/8 slice functions as a symmetry cell, which can be set up to simulate the whole motor with symmetry conditions. The symmetry cell has its periodic face aligned with the X-axis.

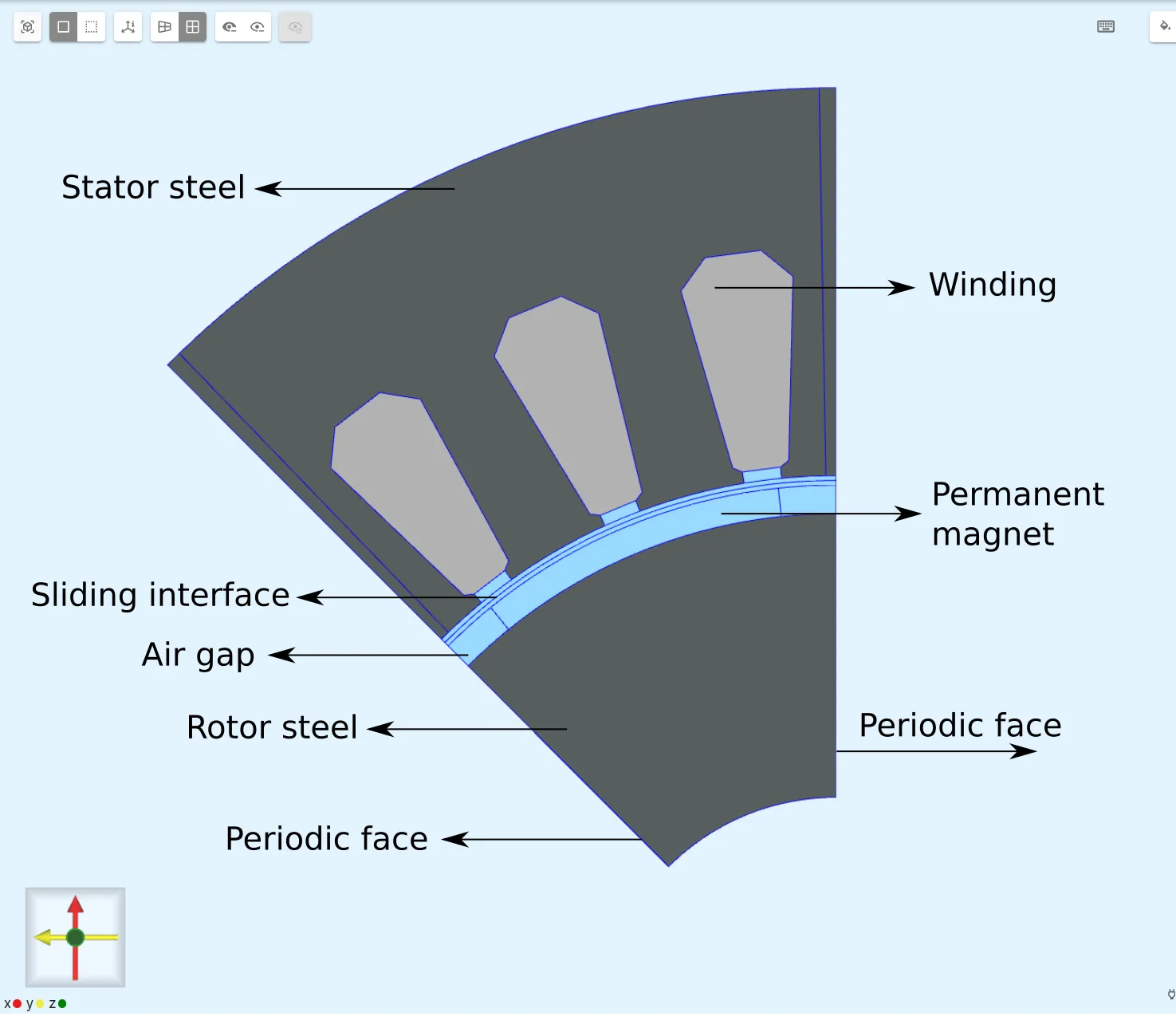
Element	Dimensions [m]
Stator steel outer radius	$0.100$
Stator steel inner radius	$0.059$
Rotor steel outer radius	$0.055$
Rotor steel inner radius	$0.025$
Permanent magnet outer radius	$0.058$
Air gap thickness	$0.001$

Material Data

• Linear steel

Property	Value
Magnetic permeability	$2000 \times \mu_0 = 2000 \times 4 \pi \times 10 ^{-7} ~ \rm H/m$

Boundary conditions

Name	Type	Value
left and right Y-planes	periodicity: rotation	antiperiodic
rotor-stator interface	continuity	potential equality on both sides

Output Results

• Torque [Nm]

Step-by-step guide

Here you’ll find a detailed step-by-step tutorial on how to simulate a permanent magnet synchronous electric motor in Quanscient Allsolve.

Step 1 - Build the geometry

Geometric entity tags

Geometric entities (volumes, surfaces, curves and points) are referenced using tags throughout this tutorial.

Carefully replicate the geometry construction steps below in order to have correct tags. Incorrect entity tags can lead to errors or unexpected behavior during simulations.

1. Start with a new project and name it PMSM Electric motor.

2. Import the STEP file containing the motor slice geometry. File download link: pmsm-electric-motor.step

   

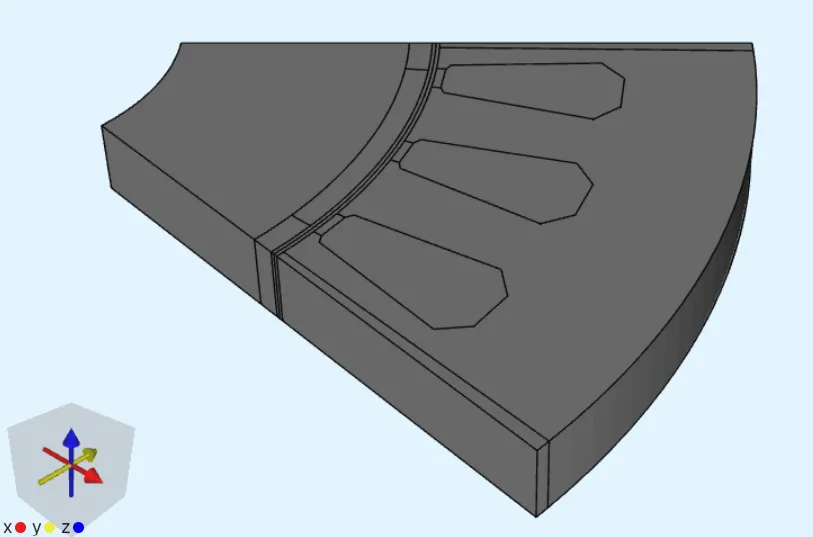
3. Add a Translate operation targetting the rotating region:

   Name	Element type	Target	Translation [m]	Copy
   translate	Translate operation	Volumes 1-5	X: 0	No
   			Y: 0
   			Z: 0.02

   Tag ordering in translate

   To ensure having the same entity tags as in this tutorial, it is crucial to order tags in the translate operation as 1, 2, 3, 4, 5.

   A failure to maintain this tag order will lead to incorrect entity tags, potentially causing errors in your simulation.

   

   The Translate operation is done in this tutorial to separate the rotor and stator for meshing, and to have a duplicate mesh on the rotor-stator interface.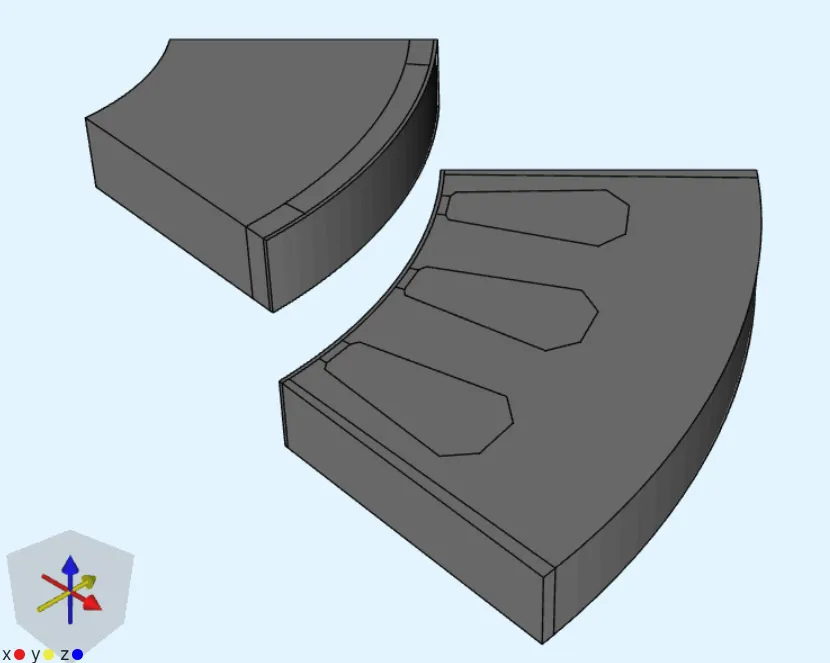

   

   The rotor is moved back into place at simulation time.

Caution: Position of geometry

In modelling a symmetry cell of a motor that has periodic boundaries:

1. The position of the geometry needs to be such that the rotation happens around the Z-axis.
2. One of the periodic boundaries needs to be aligned with the X-axis.

Step 2 - Define variables, materials and shared regions

1. Go to the Common sidebar.

2. Define variables:

   Name	Description	Expression
   I	Current amplitude [A]	300
   alpha	Mechanical angle [deg]	27
   phase	Electrical angle [deg]	0

3. Add the Air material:

   Material	Target
   Air	permanent magnet domain and all air domains (volumes 6-9, 17-20)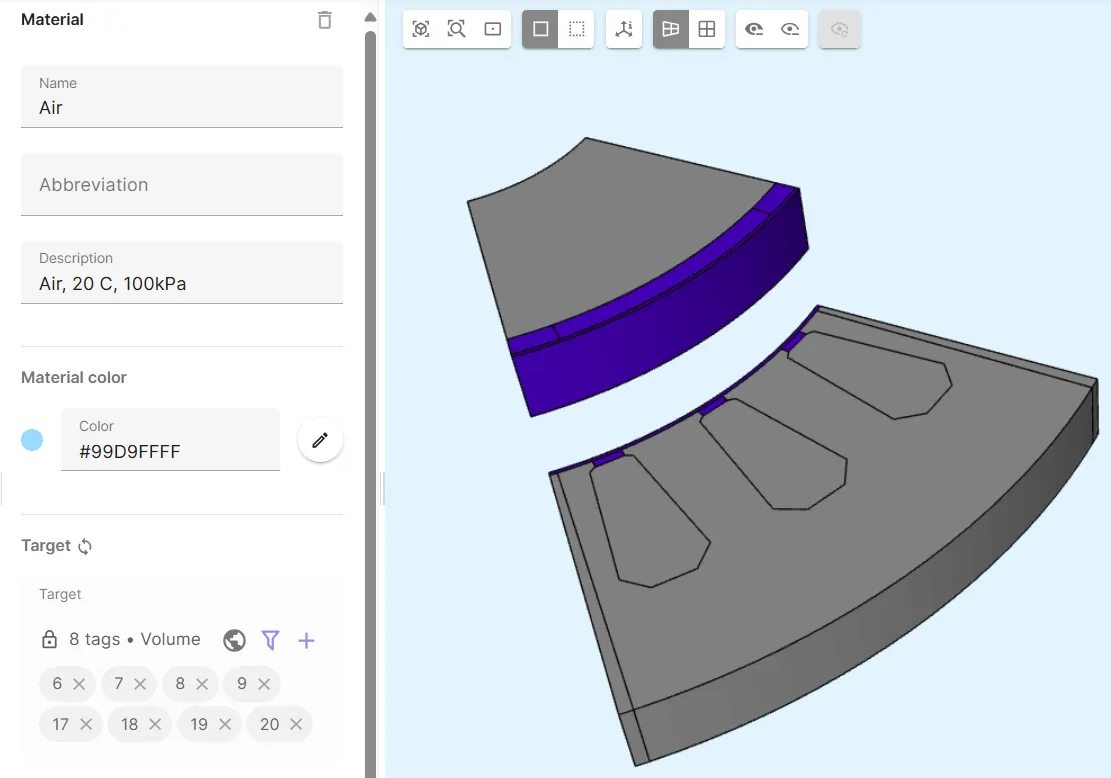

   

4. Add the Carbon steel AISI 1020 material:

   Material	Target
   Carbon steel AISI 1020	steel domain (volumes 13-16)

   

5. Instead of nonlinear permeability, linear permeability is applied to the steel in this tutorial. Edit Carbon steel AISI 1020 material properties:

   Property	Updated value
   Magnetic permeability	2000 * mu0

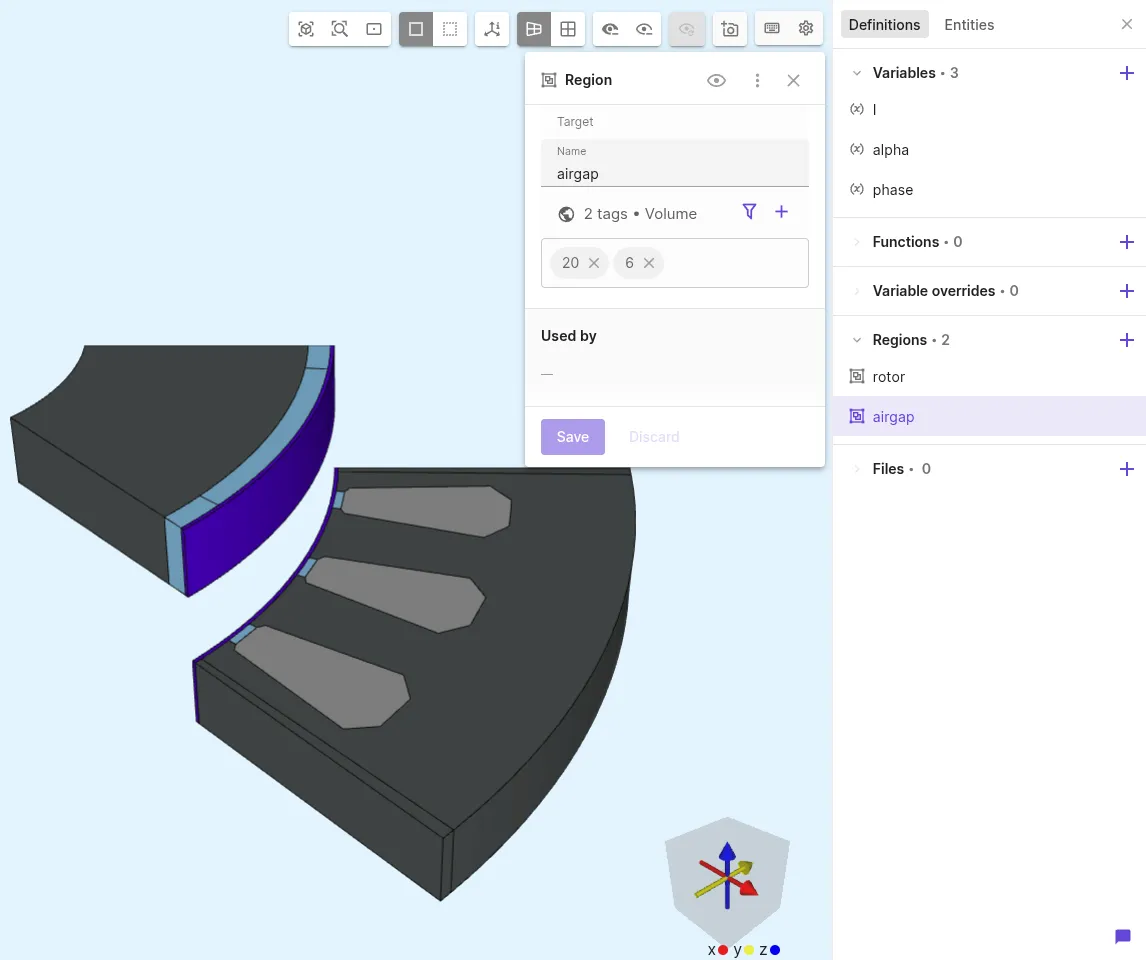
6. Define shared regions:

   Region name	Region type	Target
   rotor	Volume	all rotating regions with half of the airgap (volumes 16-20)
   airgap	Volume	volumes 6, 20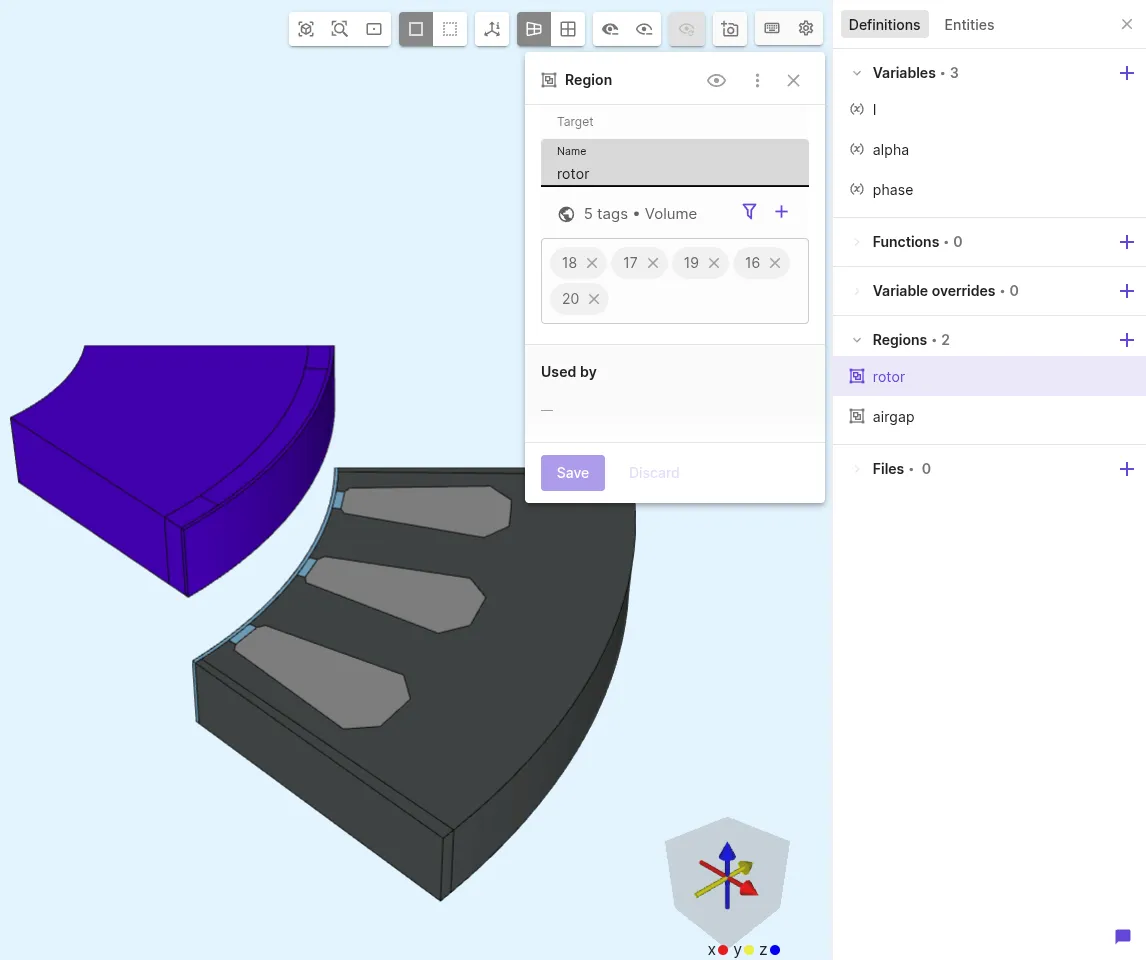

   

   

Step 3 - Define the physics and apply boundary conditions

1. Go to the Physics section.

2. Add the Magnetism φ physics:

   Physics	Target
   Magnetism φ	All volumes except the windings (volumes 6-9, 13-20)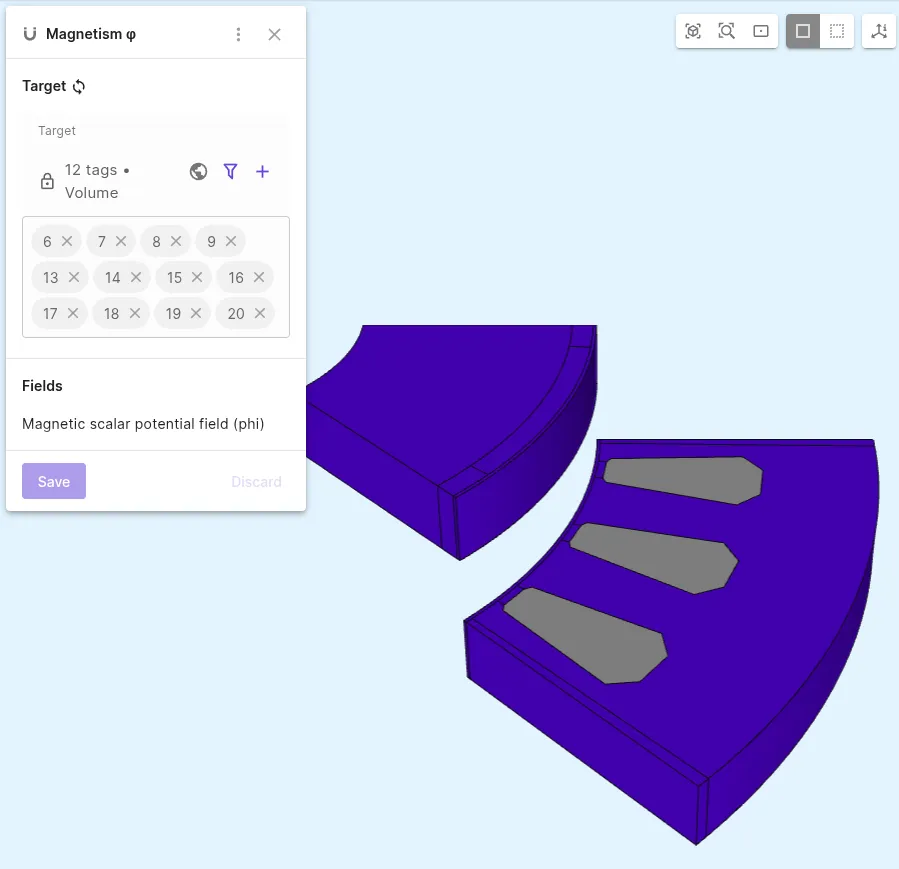

   

3. Add a Constraint interaction to Magnetism φ:

   Name	Interaction type	Target	Value
   Constraint	Constraint	a corner point on the permanent magnet	0

   This constraint is the gauge condition for the scalar potential φ. It will guarantee the uniqueness of the solution.

   

   Caution: Magnetism φ gauge condition target point

   Choose a target point on the Magnetism φ region so that it is not on the periodic boundaries nor on the sliding interface. E.g. the corner point of the permanent magnet in the air gap is a good option.

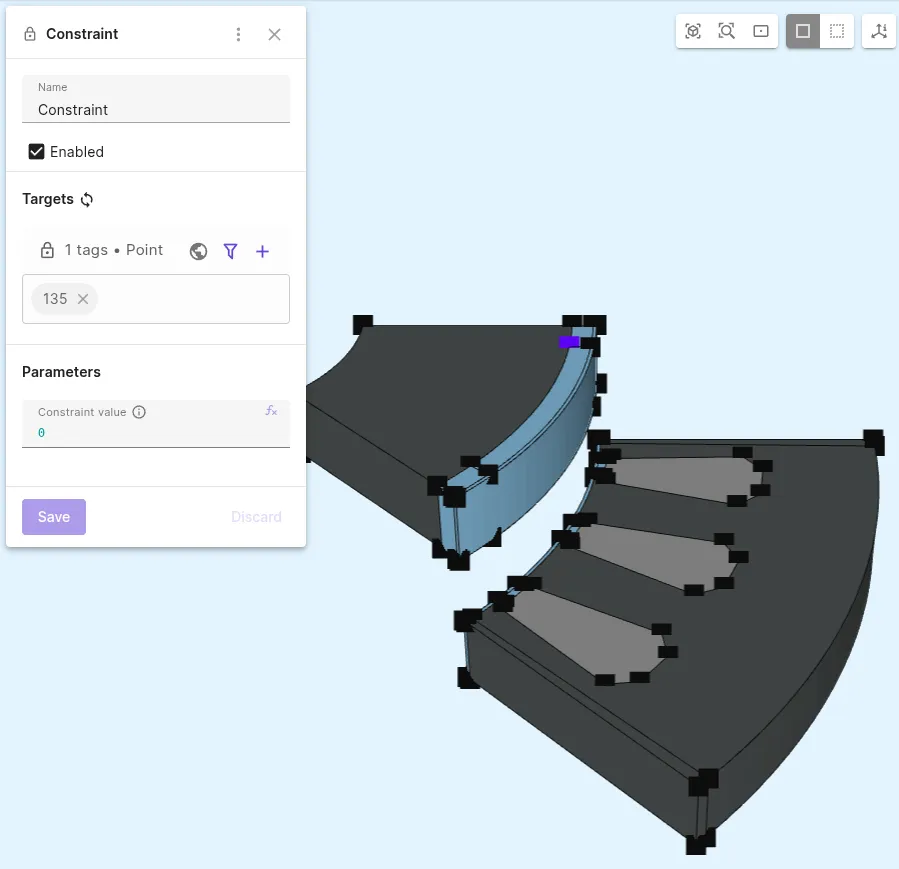
4. Add a Remanence interaction to Magnetism φ:

   Interaction name	Interaction type	Target	Value [X; Y; Z]
   Remanence	Remanence	Permanent magnet volume	[0.5*x/sqrt(x*x+y*y); 0.5*y/sqrt(x*x+y*y); 0]

   This introduces a $0.5 ~ \rm T$ radial magnetization to the motor.

   

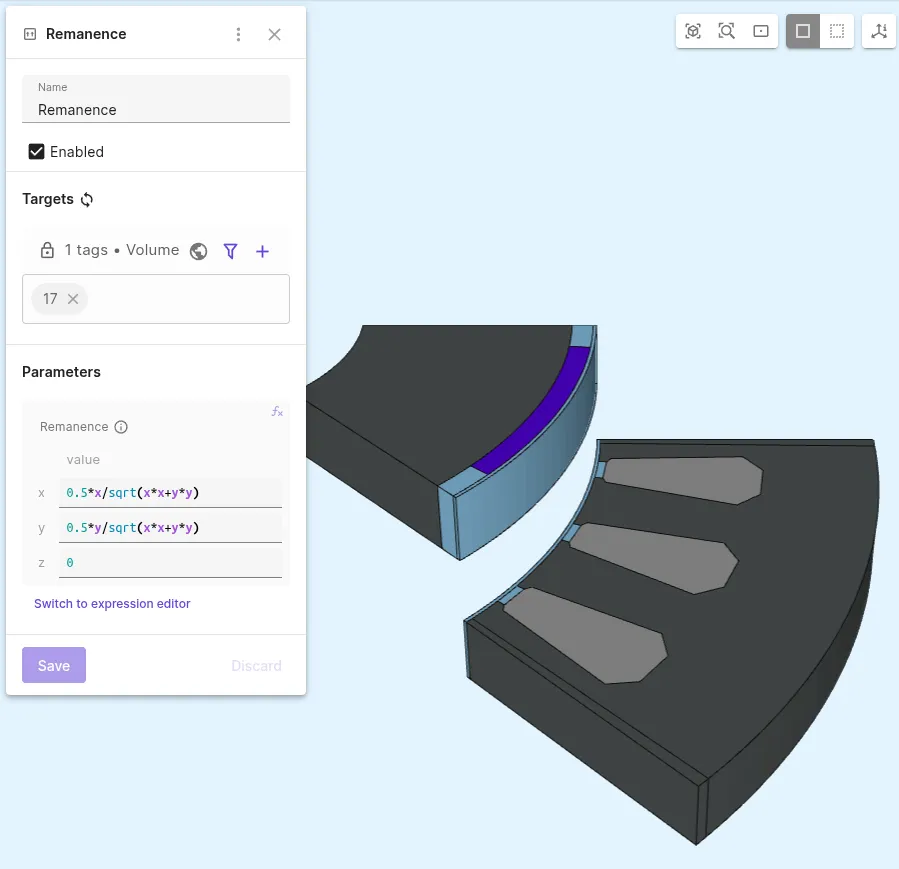
5. Add a Periodicity interaction and select target surfaces:

   Interaction name	Interaction type	Periodicity target 1	Periodicity target 2
   Periodicity	Periodicity	Side surfaces parallel to X-axis	Side surfaces opposite to target 1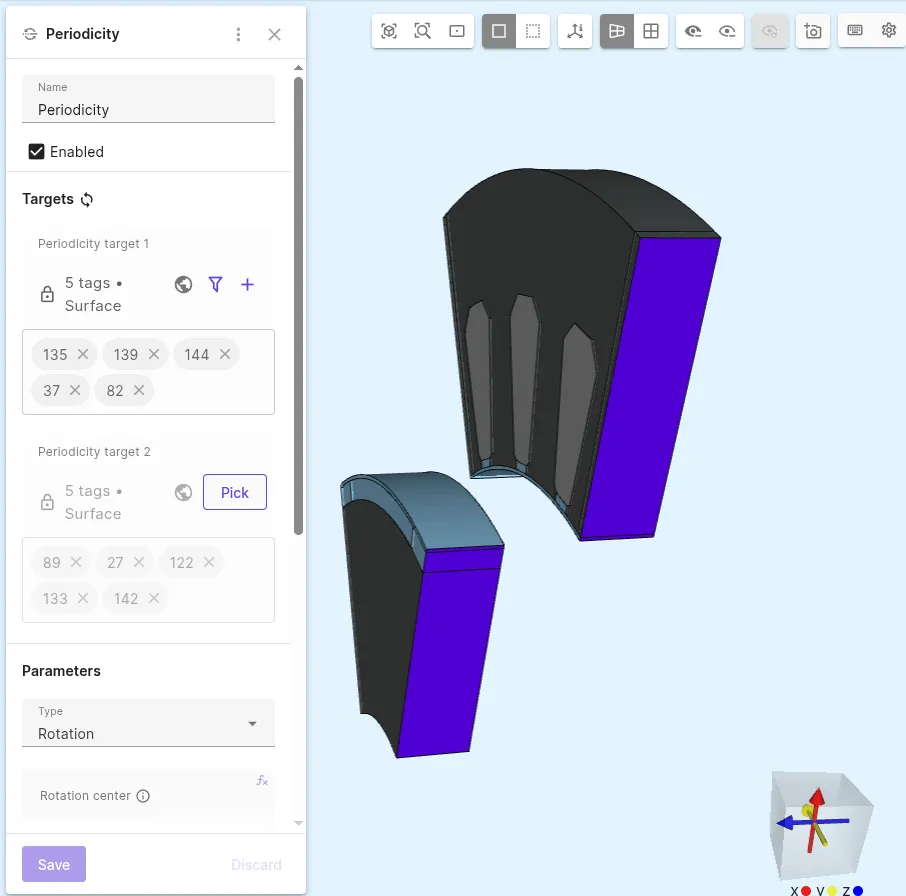

   

   

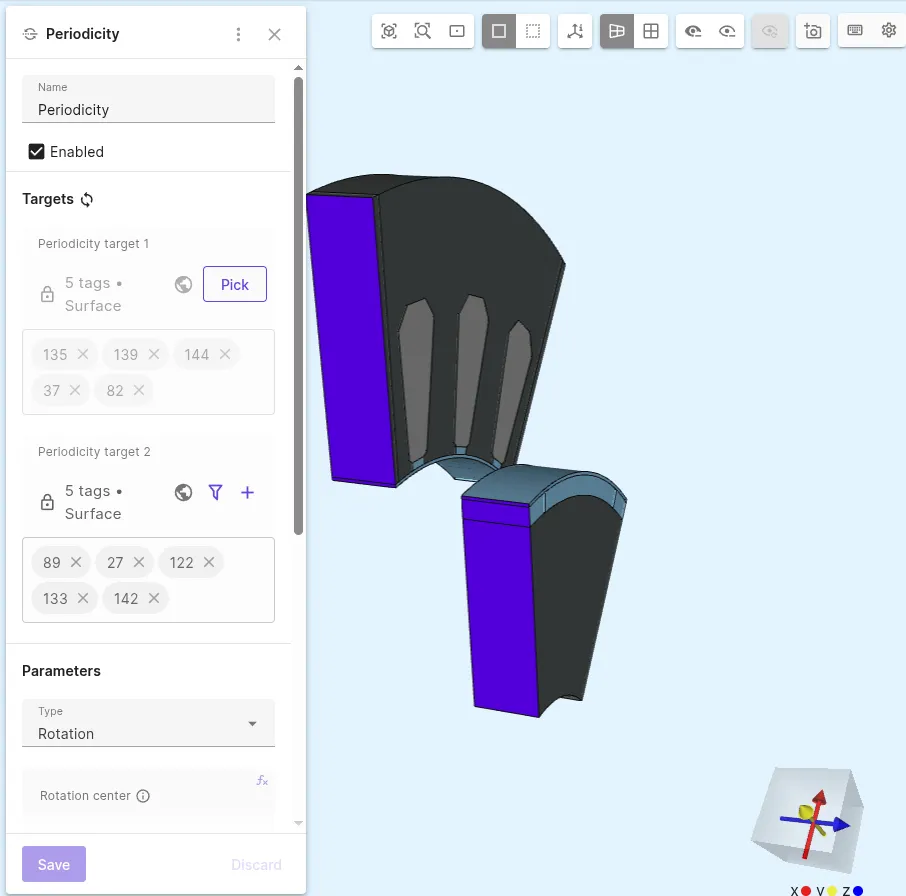
   Caution: Rotational periodicity and X-axis alignment

   When applying rotational periodicity, the first periodic surface needs to be aligned with the X-axis.

6. Select remaining options in the Periodicity interaction:

   Interaction name	Interaction type	Type	Rotation center [X; Y; Z]	Rotation angle [X; Y; Z]	Antiperiodicity
   Periodicity	Periodicity	Rotation	[0; 0; 0]	[0; 0; 45]	Yes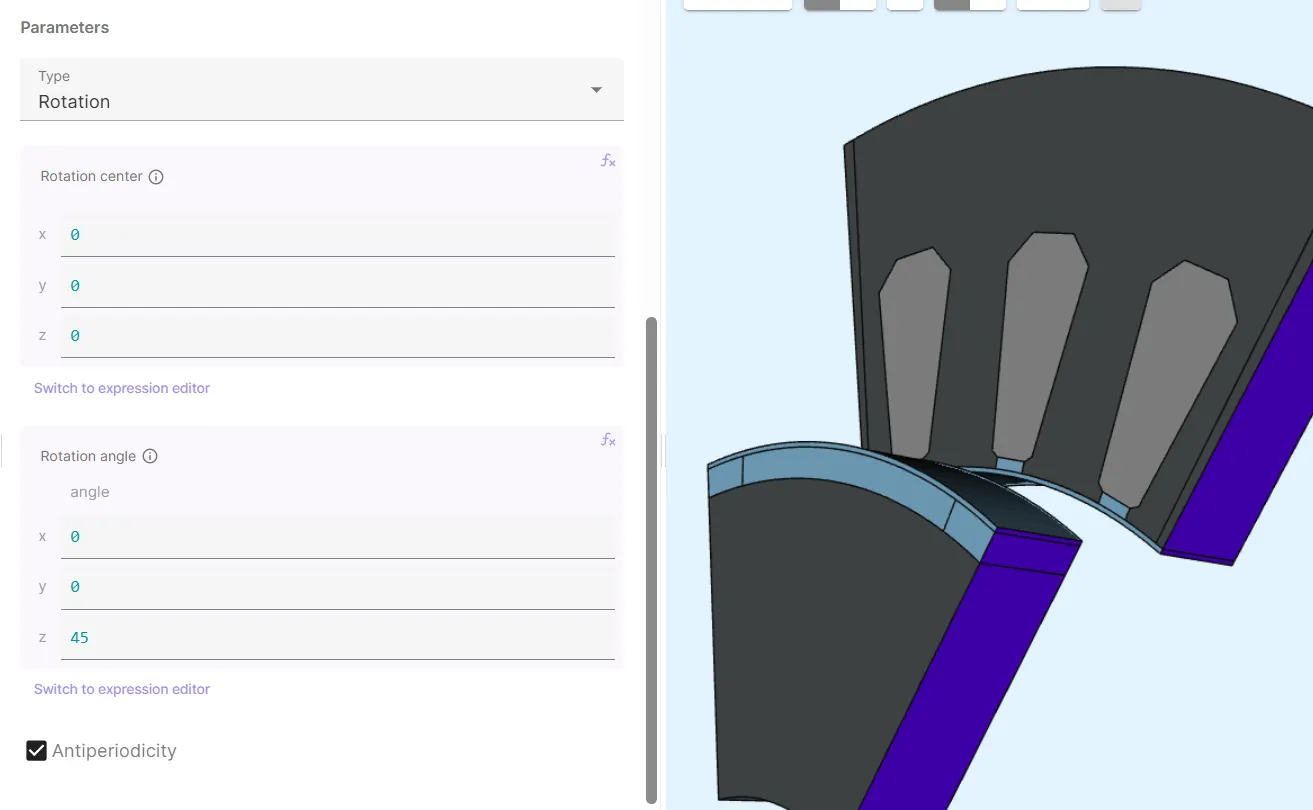

   

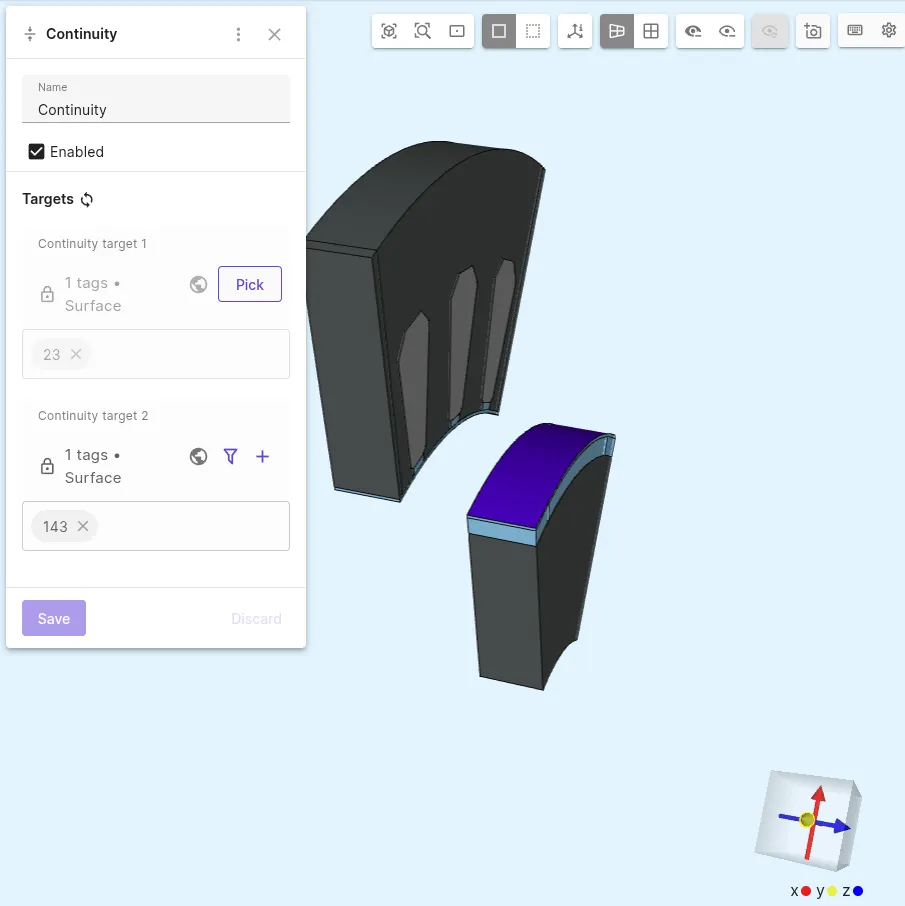
7. Add a Continuity interaction:

   Interaction name	Interaction type	Continuity target 1	Continuity target 2
   Continuity	Continuity	Stator interface surface 23	Rotor interface surface 143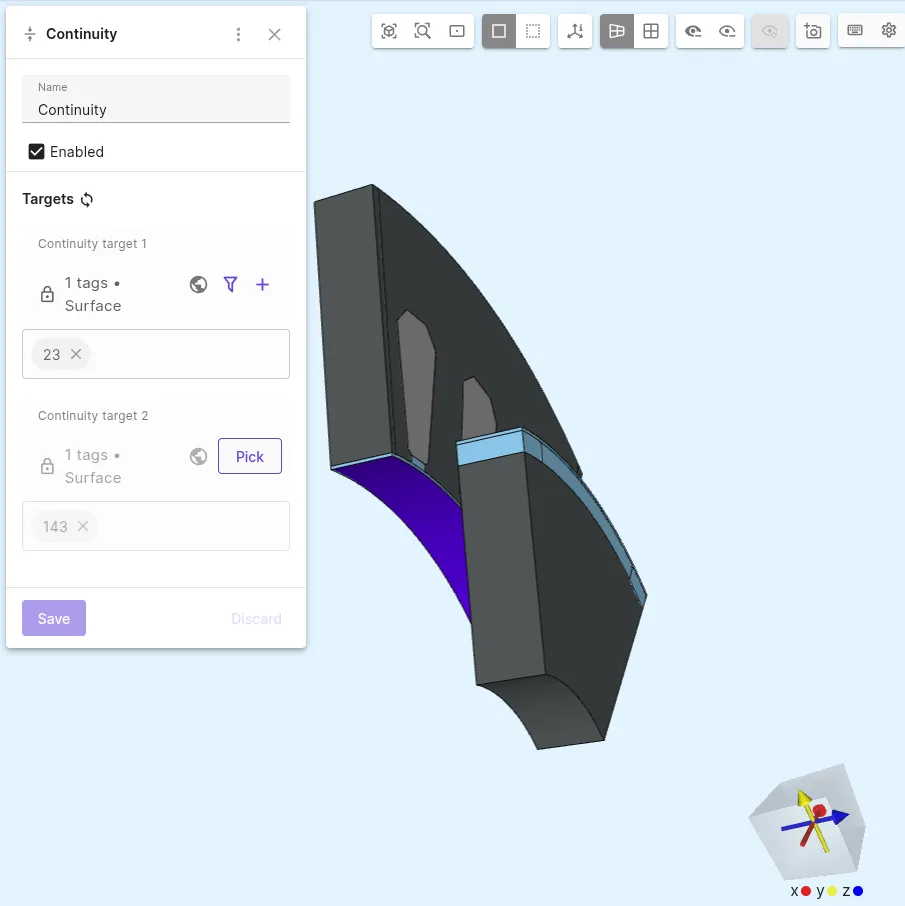

   

   

8. Add Lump I/V cut interactions to introduce current sources on the windings:

   Interaction name	Interaction type	Target	Actuation mode	Current
   Lump I/V cut	Lump I/V cut	Counterclockwise loop around left-most winding	Current	I * sin((phase + 4.0 * alpha - 120.0) * pi/180.0)
   Lump I/V cut 2	Lump I/V cut	Counterclockwise loop around middle winding	Current	I * sin((phase + 4.0 * alpha - 60.0) * pi/180.0)
   Lump I/V cut 3	Lump I/V cut	Counterclockwise loop around right-most winding	Current	I * sin((phase + 4.0 * alpha - 0.0) * pi/180.0)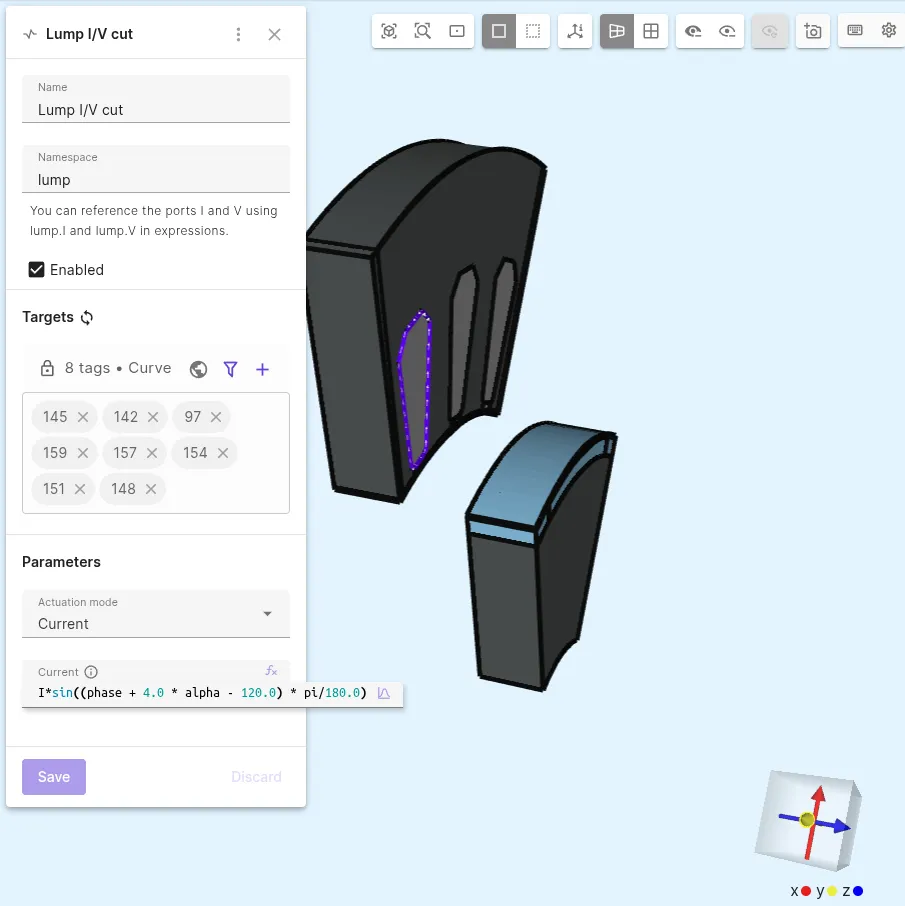

   

   

   

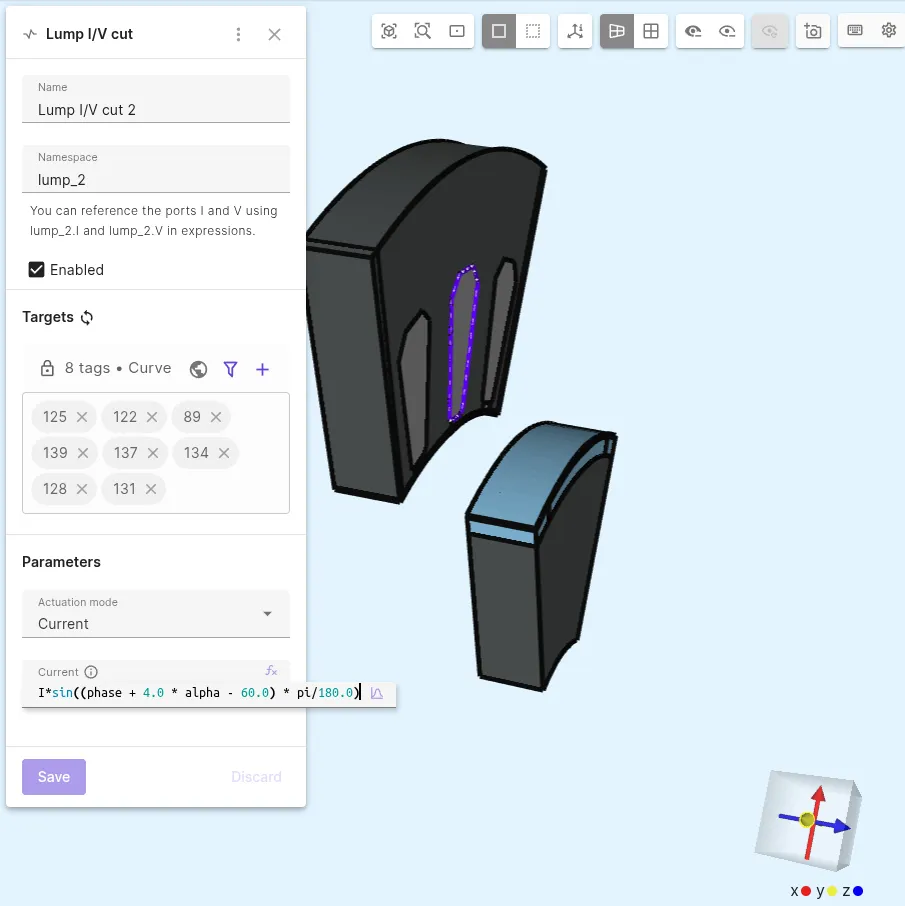
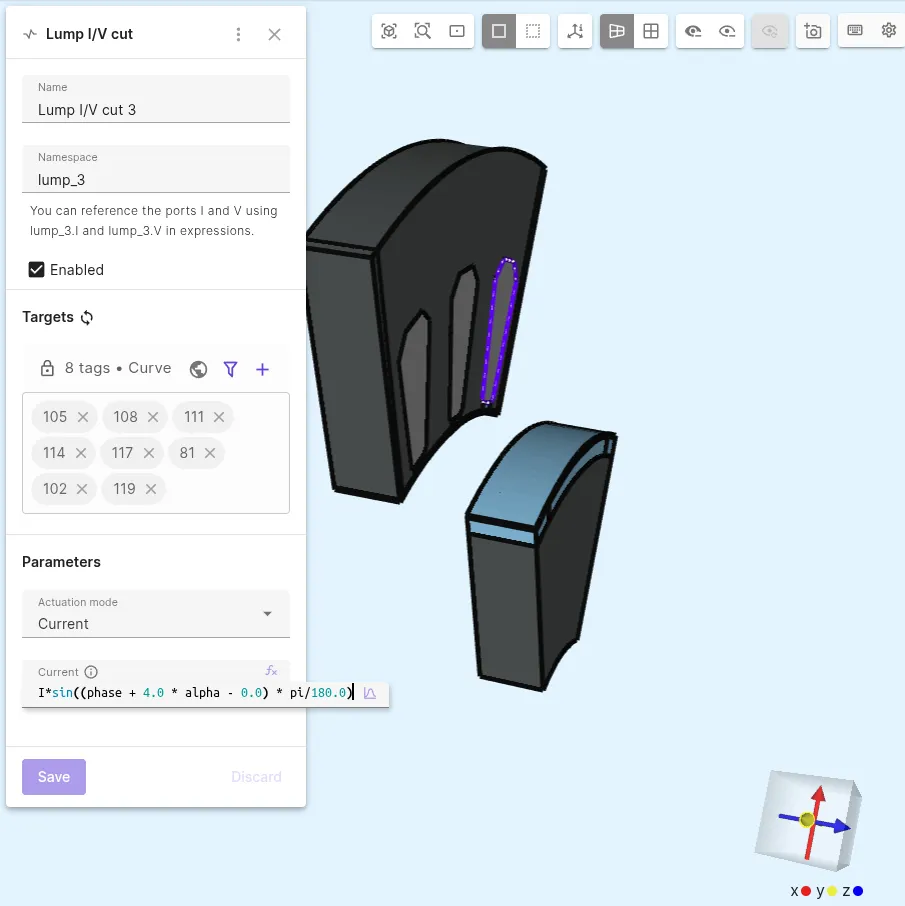
   Note: Electrical angle

   Here, the rotor has 8 poles. Therefore, the electrical angle is 8/2 times the mechanical angle at a synchronous speed.

There are 7 interactions in total:

Step 4 - Generate the mesh

1. Go to the Simulations section.

2. Create a new mesh.

3. Set mesh quality to Expert settings.

4. Set mesh element max size to 0.001.

5. Enable Curved mesh.

6. Add a mesh refinement entity:

   Mesh refinement entity type	Target	Max size
   Volume	air gap volumes	0.0005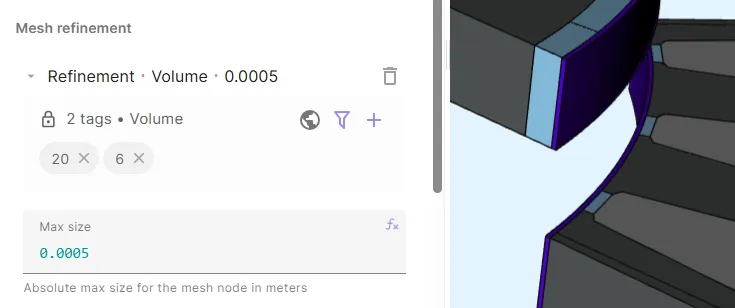

   

7. Apply settings and generate the mesh.

8. Check the preview:

   

Step 5 - Apply simulation settings

1. Create a new simulation.

2. Set Analysis type to Steady state.

3. Select Mesh 1 as the mesh for your simulation.

4. Add a magnetic flux density B field output. As target, select all volumes except the windings.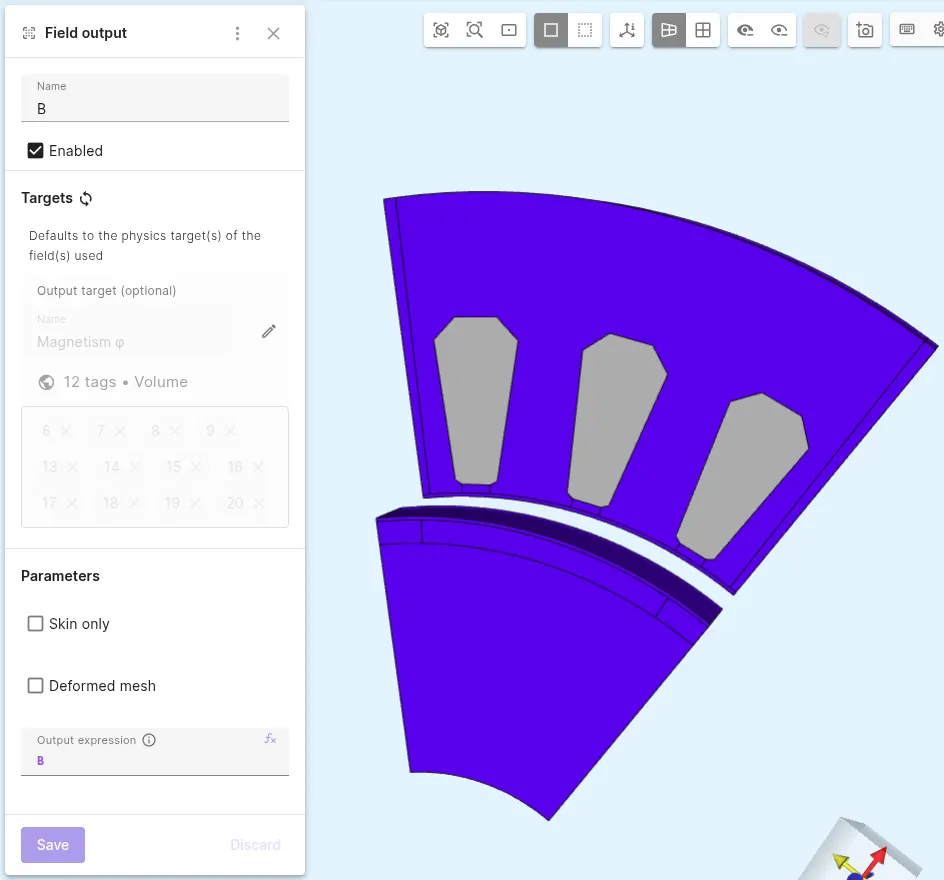

   

Step 6 - Modify the script

The following modifications need to be done by scripting:

• Move the rotor back to its original position and apply rotation.
• Apply antioperiodicity and rotation for the continuity condition.
• Calculate the torque.

To do these modifications, do the following:

1. Open the script for your simulation.

2. Enable scripting mode.

3. Add these lines to the script right below the initial mesh loading stage:

   # Moving the rotor back to it's original position and applying rotation
   mesh.mesh.shift(reg.rotor, 0.0, 0.0, -0.02)
   mesh.mesh.rotate(reg.rotor, 0.0, 0.0, expr.alpha)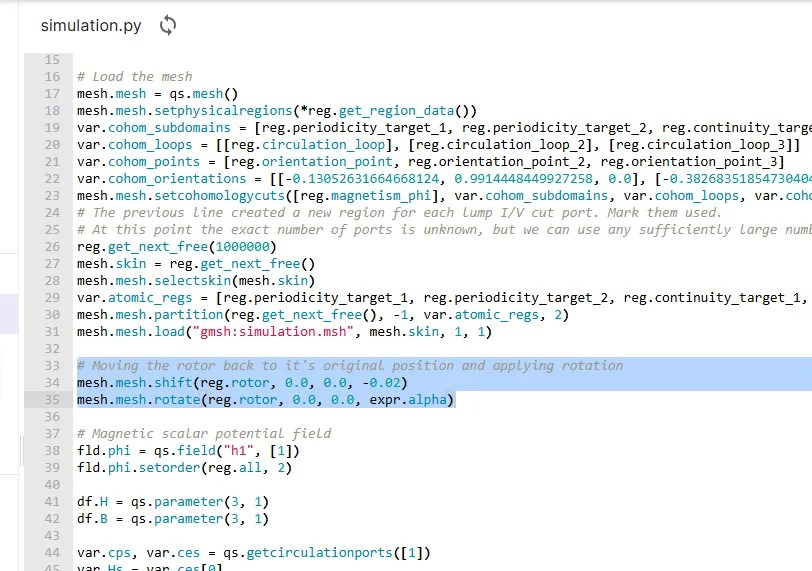

   

4. To address the antiperiodicity regarding the rotated position for the continuity condition, add the following arguments on the continuitycondition() function:

   qs.continuitycondition(..., [0,0,0], expr.alpha, 45.0, -1.0)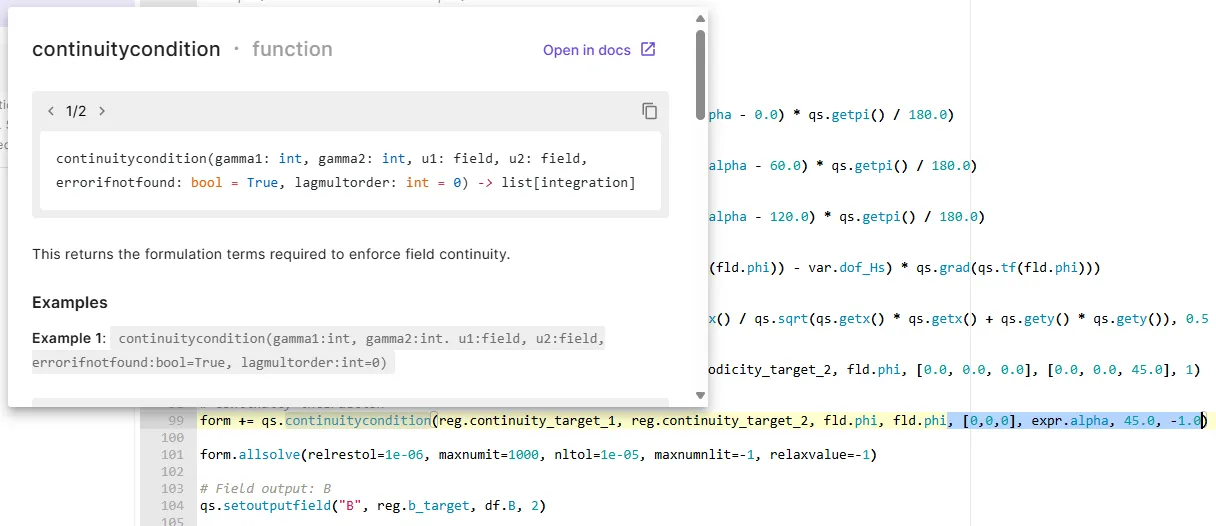

   

5. To calculate the torque via Arkkio’s method ¹ and via Maxwell’s Stress Tensor, add the following lines to the very end of the script:

   # Calculating torque:
   
   # The torque is scaled (8*5) to the actual z length of the motor 0.05 m and to take into account full 360 degrees of the motor.
   
   # 1) Using Arkkio's method
   rs = 0.059 # outer radius of airgap
   rr = 0.058 # inner radius of airgap
   radius = qs.sqrt( qs.pow(qs.getx(),2) + qs.pow(qs.gety(),2) )
   ephi = qs.array3x1(-qs.gety()/radius, qs.getx()/radius, 0.0)
   er = qs.array3x1(qs.getx()/radius, qs.gety()/radius, 0.0)
   Bphi = df.B*ephi
   Br = df.B*er
   dr = (rs-rr)
   magforcedensity1 = (8*5*radius*Br*Bphi/qs.getmu0()/dr)
   torque1 = magforcedensity1.allintegrate(reg.airgap,5)
   
   # 2) Using Maxwell stress tensor
   leverarm = qs.array3x1(qs.getx(), qs.gety(), 0.0)
   T = 1/qs.getmu0() * ( df.B*qs.transpose(df.B) - 0.5*df.B*df.B * qs.eye(3) )
   magforcedensity2 = qs.on(reg.airgap, T)*qs.normal(reg.airgap)
   torque2 = 8*5*qs.compz(qs.crossproduct(leverarm, magforcedensity2)).allintegrate(reg.continuity_target_2, 5)
   
   qs.setoutputvalue("Mechanical angle", qs.evaluate(expr.alpha)[0])
   qs.setoutputvalue("Torque (Arkkio)", qs.evaluate(torque1))
   qs.setoutputvalue("Torque (Maxwell's Stress Tensor)", qs.evaluate(torque2))

6. Save the script.

Step 7 - Running the simulation and checking results

1. Run Simulation 1.

2. To follow the simulation progress, open the Logs.

   

3. Once the simulation has finished, add a B field visualization.

4. Add a Glyph filter to the visualization:

   Filter	Layer	Max sample points	Scaling mode	Scale factor
   Glyph	B - Cool to Warm	50000	data	0.005
   	0.0002 - 1.0

5. Activate the visualization.

   

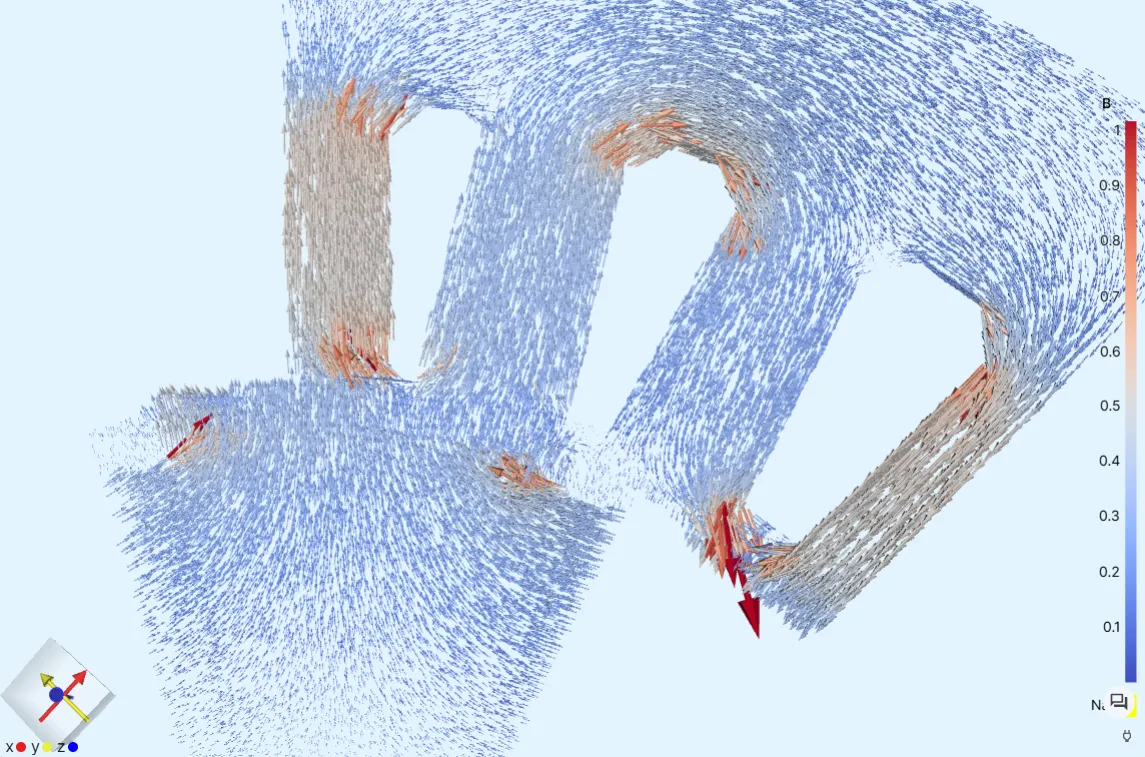
6. To see the value of torque [Nm] at the applied mechanical angle [deg], see the Summary.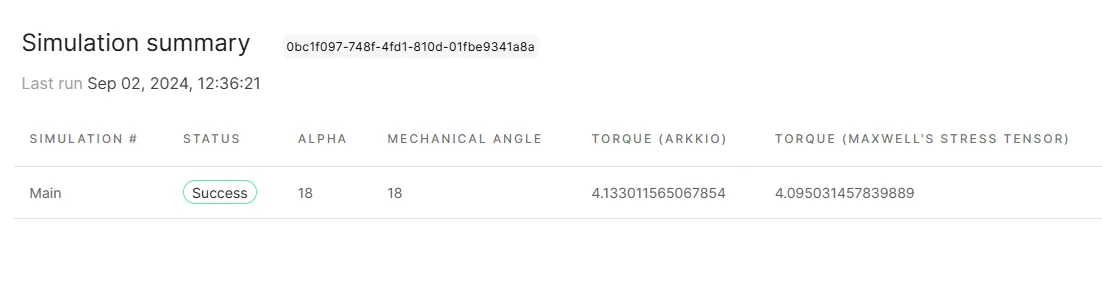

   

References

Footnotes

1. Arkkio’s Method for Torque Computation, https://www.anttilehikoinen.fi/research-work/arkkios-method-torque-computation/ ↩