Pull-in analysis of a MEMS device

In this tutorial, pull-in analysis is simulated for a MEMS device.

Pull-in analysis is performed to determine the pull-in voltage of a MEMS device. At this voltage, the device becomes unstable as the electrostatic forces can no longer be balanced by the stiffness of the device.

Model definition

The model consists of two parallel square plates with a certain thickness, separated by a vacuum gap. A DC voltage is applied to the bottom plate while the top plate is grounded. The bottom plate is clamped and the top plate is attached to a spring with stiffness $K$. The displacement of the top plate is constrained to move only in the $Z$-direction. The interaction between the top plate and attached spring is determined using a lumped model:

$$F_z = -K \cdot U_z$$

Parameters

The model parameters, that should be defined as variables in Allsolve, are defined as follows:

• Length of the square plate, $L = 50$ μm
• Height of the square plate, $H = 3$ μm
• Gap between the two parallel square plates, $d = 1$ μm
• Stiffness of the spring, $K = 10000$ N/m
• Overlapping area between the two parallel plates, $A = L \times L ~$ m²

Geometric elements

Element	Size	Center point (X, Y, Z)
Bottom plate	L $\times$ L $\times$ H	(0, 0, 0)
Top plate	L $\times$ L $\times$ H	(0, 0, H + d)
Vacuum box	L $\times$ L $\times$ d	(0, 0, H/2 + d/2)

Output Results

• Plot of applied voltage vs resulting displacement.

Material Data

1. Vacuum for the gap between the parallel plates
   • Electric permittivity: $\epsilon$ = $\epsilon_0 ~$ [F/m]
2. Silicon dioxide for the top and bottom plate
   • Young’s modulus: $E$ = $70 ~$ [GPa]
   • Poisson’s ratio: $\nu$ = $0.17$
   • Electric permittivity: $\epsilon$ = $3.9 \cdot \epsilon_0 ~$ [F/m]

Note: Electric permittivity in a vacuum

$\epsilon_0$ = $\dfrac{1}{\mu_0 c^2}$ = $8.854 \cdot 10^{-12} ~$ F/m

Boundary conditions

• Bottom plate

  • Electrode: $V$ = $V_{\rm DC}$
  • Clamped: $[u_x, u_y, u_z]$ = $[0, 0, 0]$

• Top plate

  • Grounded: $V$ = $0$
  • in-plane clamp: $[u_x, u_y]$ = $[0, 0]$

Note

A variable called Vdc will be defined in Allsolve, which provides a temporary value for the voltage. Later, this variable is swept over by defining a sweep override which takes a vector of voltage values.

Analytical solution

For the model setup defined above, the analytical solution to the pull-in voltage $V_{\rm p}$ is given by the formula: ¹

$$V_{\rm p} = \sqrt{\frac{8}{27}\frac{Kd^3}{\epsilon A}}$$

where,

• $K$ is the spring stiffness [N/m].
• $d$ is the initial gap between the parallel plates [m].
• $\epsilon$ is the electric permittivity of the gap medium [F/m].
• $A$ is the overlapping area between the parallel plates [m²].

The corresponding displacement $u_{\rm p}$ of the top plate at pull-in voltage is one-third of the initial gap between the plates.

$$x = \frac{1}{3} d$$

The pull-in voltage and the corresponding displacement based on the values defined in Parameters:

$$V_{\rm p} = 365.9 ~ volts \\ u_{\rm p} = 0.3333 ~ μm$$

Step-by-step guide

Here you’ll find a detailed step-by-step tutorial on how to simulate this in Quanscient Allsolve

Step 1 - Build the geometry

Geometric entity tags

Geometric entities (volumes, surfaces, curves and points) are referenced using tags throughout this tutorial.

Carefully replicate the geometry construction steps below in order to have correct tags. Incorrect entity tags can lead to errors or unexpected behavior during simulations.

1. Start with a new project, and name it as Pull-in analysis.

2. In the project starting options dialog, choose box as a starting point.

3. Finish model editing for now and go to the Common sidebar.

4. Add variables:

   Name	Description	Expression
   L	Plate size [m]	50e-6
   H	Plate thickness [m]	3e-6
   d	Gap between plates [m]	1e-6
   Vdc	DC Voltage [V]	1
   K	Spring stiffness [N/m]	1e4
   A	Overlap area between plates [m]	L*L

5. Go back to the Geometry section to finish model editing.

6. Change the box size (X; Y; Z) to (L; L; H):

   Name	Element type	Center point [m]	Size [m]	Rotation [deg]
   box	Box	X: 0	X: L	X: 0
   		Y: 0	Y: L	Y: 0
   		Z: 0	Z: H	Z: 0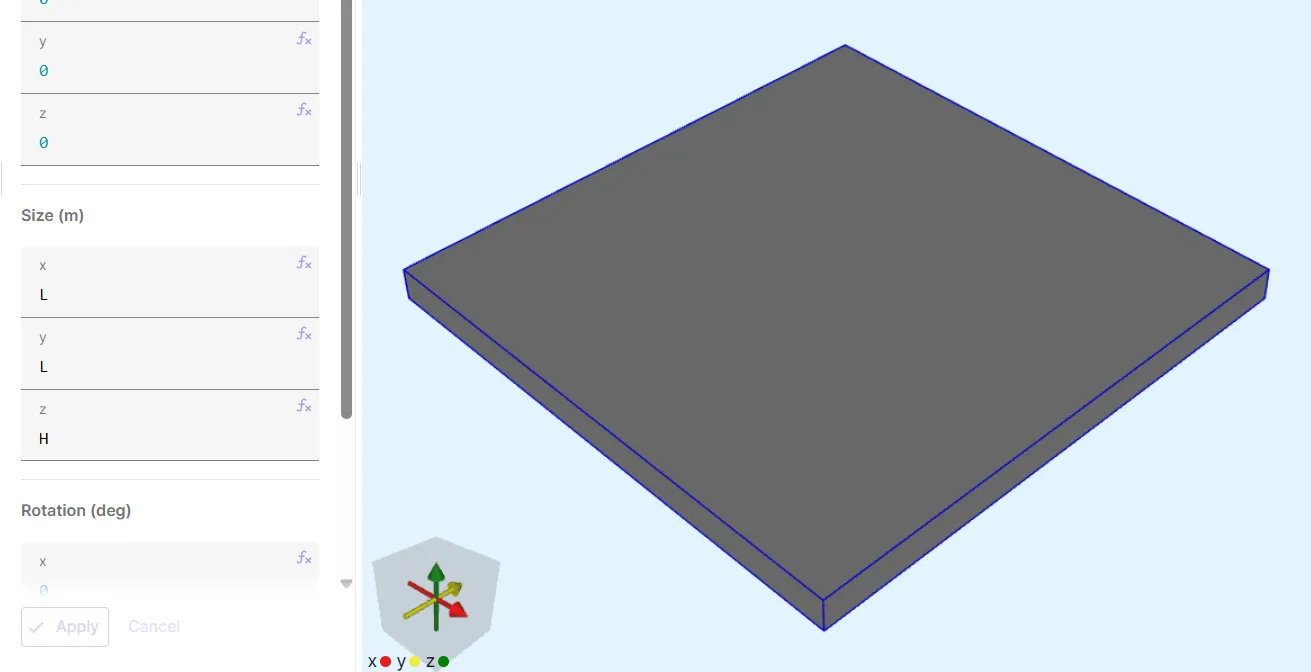

   

7. To build the other parallel plate, use the Translate geo operation:

   Name	Element type	Target	Translation [m]	Copy	Repeat count
   translate	Translation	Volume 1	X: 0	Yes	1
   			Y: 0
   			Z: H + d

8. Confirm the settings and build the translation.

   

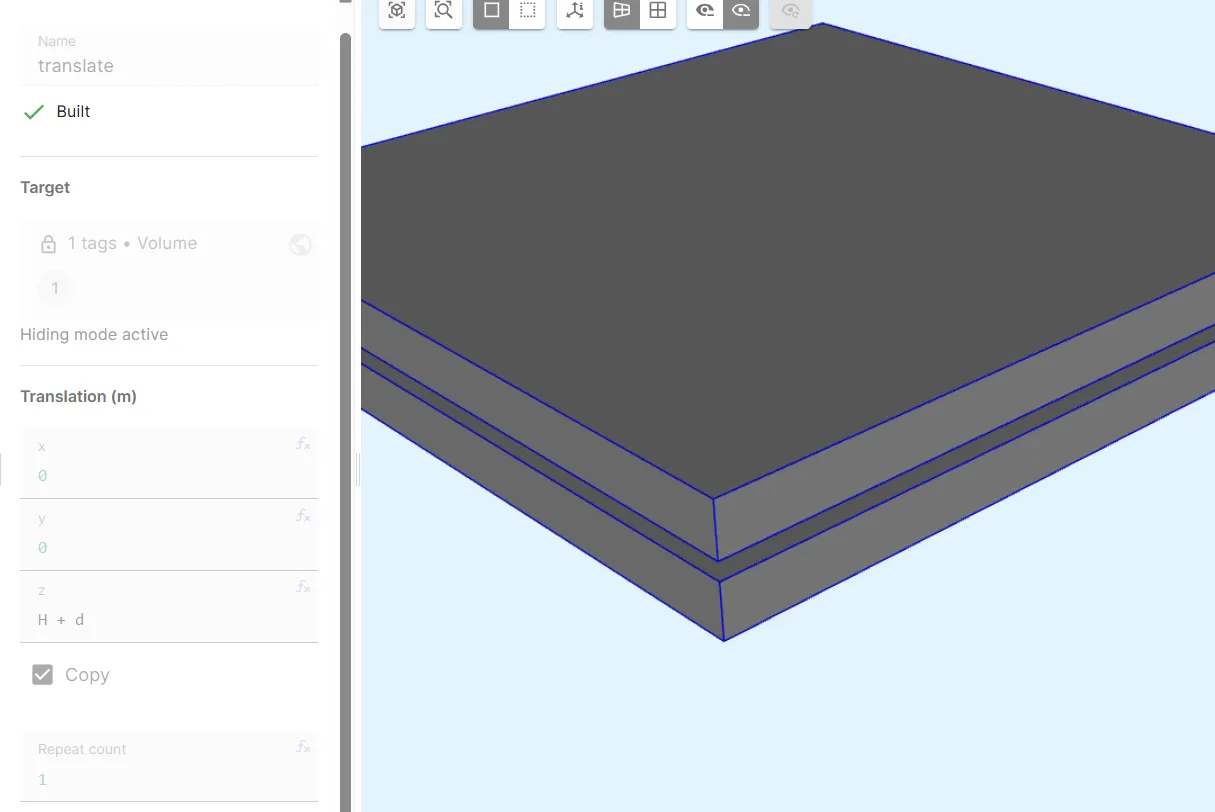
9. To fill the gap between the parallel plates, build another box:

   Name	Element type	Center point [m]	Size [m]	Rotation [deg]
   box 2	Box	X: 0	X: L	X: 0
   		Y: 0	Y: L	Y: 0
   		Z: H/2 + d/2	Z: d	Z: 0

Your geometry is now finished.

Step 2 - Define the materials

1. Go to the Common sidebar.

2. Add the Vacuum material and assign it to the gap between the plates (volume 25). Add the target region as a shared region.

3. Add the Silicon dioxide material and assign it to the plates (volumes 1, 2). Add the target as a shared region.

Step 3 - Define physics and interactions

1. Go to the Physics section.

2. Add the Solid Mechanics, Electrostatics and Mesh deformation physics.

   Tip: Physics

   It is useful to add all physics first, and then move on to defining their interactions.

   Some interactions, such as couplings, require all physics to be added first, before the interaction can be defined.

Physics 1 - Solid mechanics

1. Select the silicon dioxide shared region (volumes 1, 2) as solid mechanics target.

   Physics	Target
   Solid mechanics	Silicon dioxide region (volumes 1, 2)

2. Add a Clamp interaction to Solid mechanics.

   Interaction name	Interaction type	Target	Value
   Clamp	Clamp	Bottom plate (volume 1)

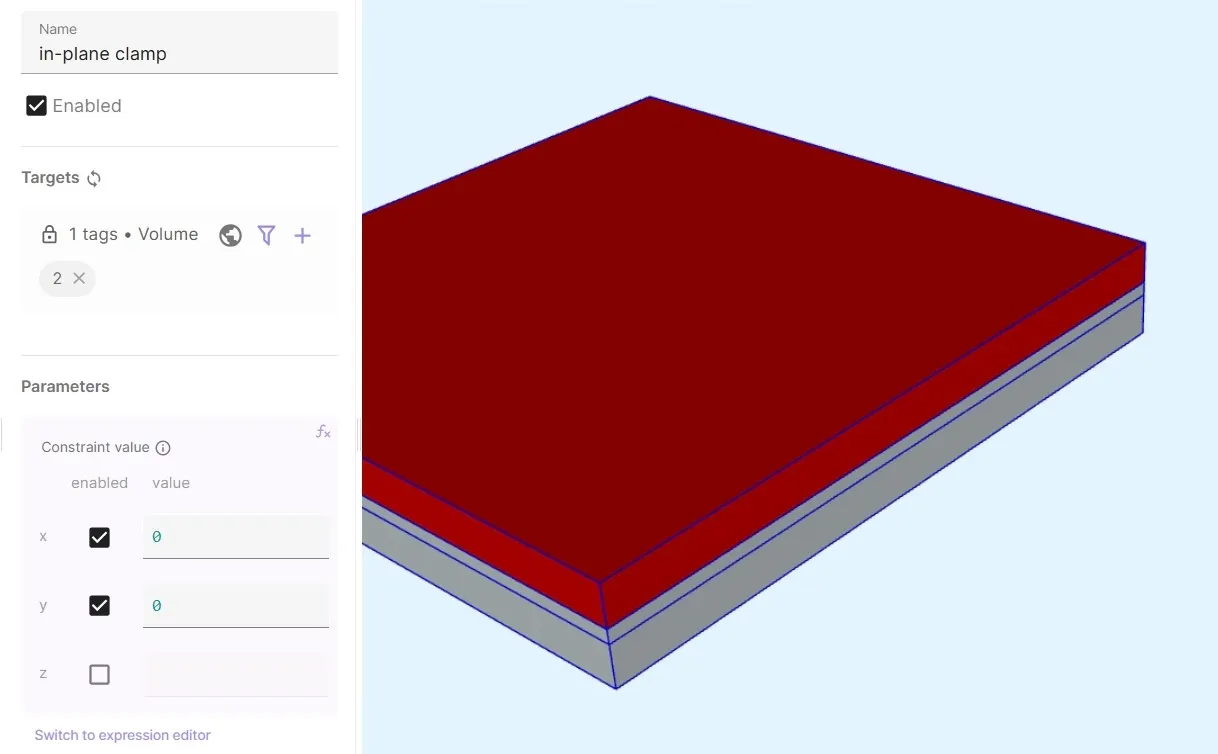
3. Add a Constraint interaction to Solid mechanics:

   Interaction name	Interaction type	Target	Value
   in-plane clamp	Constraint	Top plate (volume 2)	[1, 0; 1, 0; 0, 0]

   The in-plane clamp interaction is used to constraint the movement of the top plate in X and Y directions. Z-directional movement is left unconstrained.

   

4. Add Lump U/F to Solid mechanics:

   Interaction name	Interaction type	Target	Actuation mode	Value
   Lump U/F	Lump U/F	Top plate top surface (surface 12)	Circuit coupling	[0, 0; 0, 0; 1, lump.Fz + K*lump.Uz]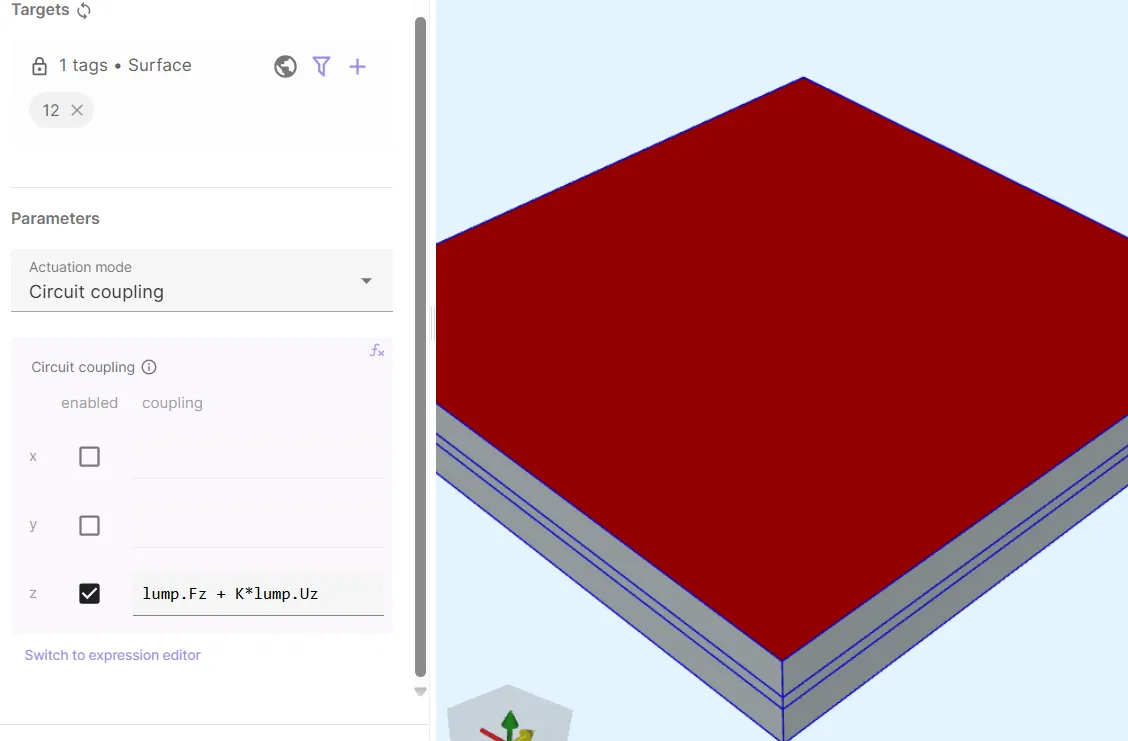

   

   Lump U/F is used to attach a spring to the top surface of the top plate via circuit coupling.

5. Add the Electric force interaction, which couples Solid mechanics to Electrostatics.

6. Add the Large displacement interaction, which couples Solid mechanics to Mesh deformation.

Physics 2 - Electrostatics

1. Let the electrostatics target default to the whole geometry.

   Physics	Target
   Electrostatics	All volumes (1, 2, 25)

2. Add a Constraint interaction to Electrostatics.

   Interaction name	Interaction type	Target	Value
   ground	Constraint	Top plate (volume 2)	0

3. Add another Constraint interaction to Electrostatics:

   Interaction name	Interaction type	Target	Value
   electrode	Constraint	Bottom plate (volume 1)	Vdc

4. Add the Large displacement interaction, which couples Electrostatics to Mesh deformation.

Physics 3 - Mesh deformation

1. Let the mesh deformation target default to the whole geometry.

   Physics	Target
   Mesh deformation	All volumes (1, 2, 25)

2. Add a Constraint interaction to Mesh deformation:

   Interaction name	Interaction type	Target	Value
   Constraint	Constraint	Silicon dioxide target (volumes 1, 2)	[1, compx(u); 1, compy(u); 0, compz(u)]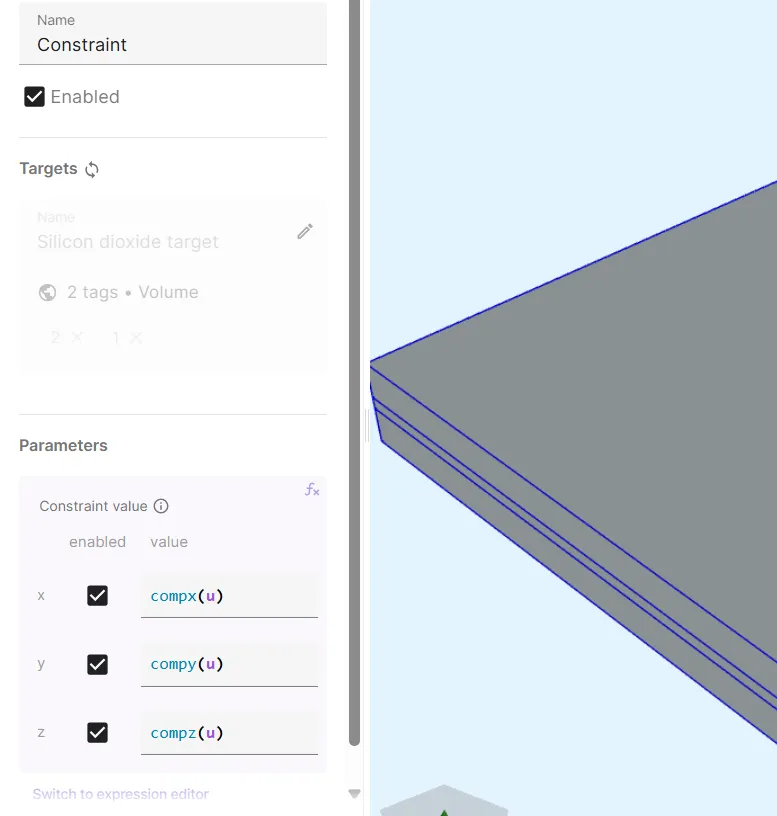

   

3. Add another Constraint interaction to Mesh deformation:

   Interaction name	Interaction type	Target	Value
   in-plane constraint	Constraint	Vacuum gap (volume 25)	[1, 0; 1, 0; 0, 0]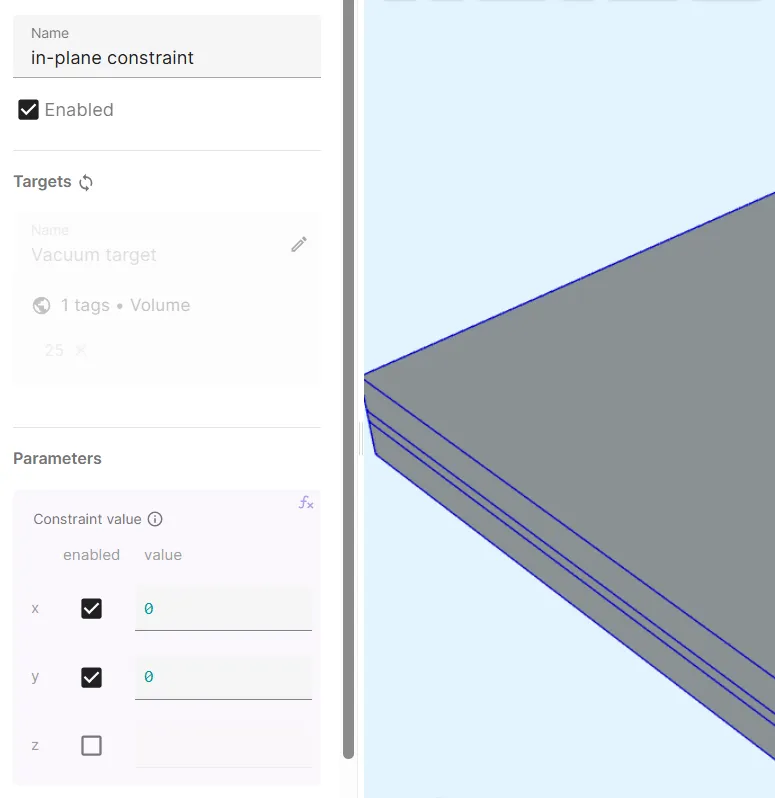

   

All your physics and interactions are now added.

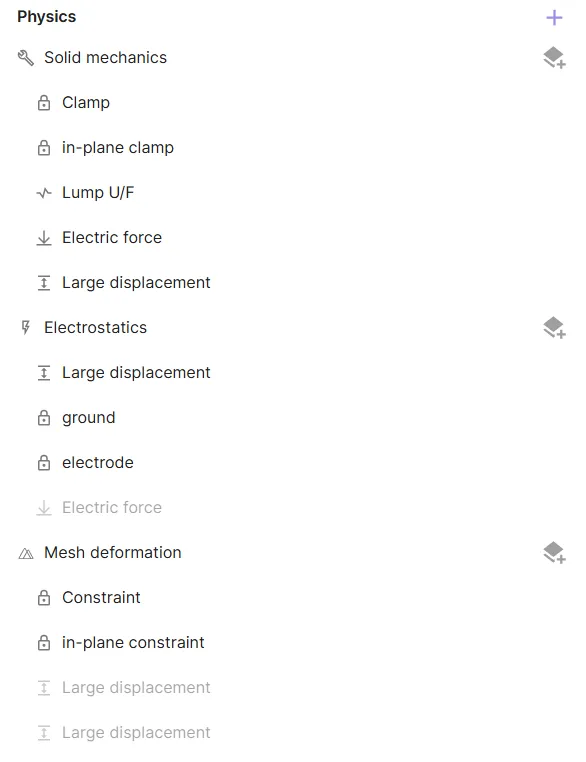
Step 4 - Generate the mesh

1. Go to the Simulations section.

2. Add a new mesh.

3. Set Mesh quality to Expert Settings.

4. Set Used Mesher to Basic.

5. Set Scale factor to 0.75.

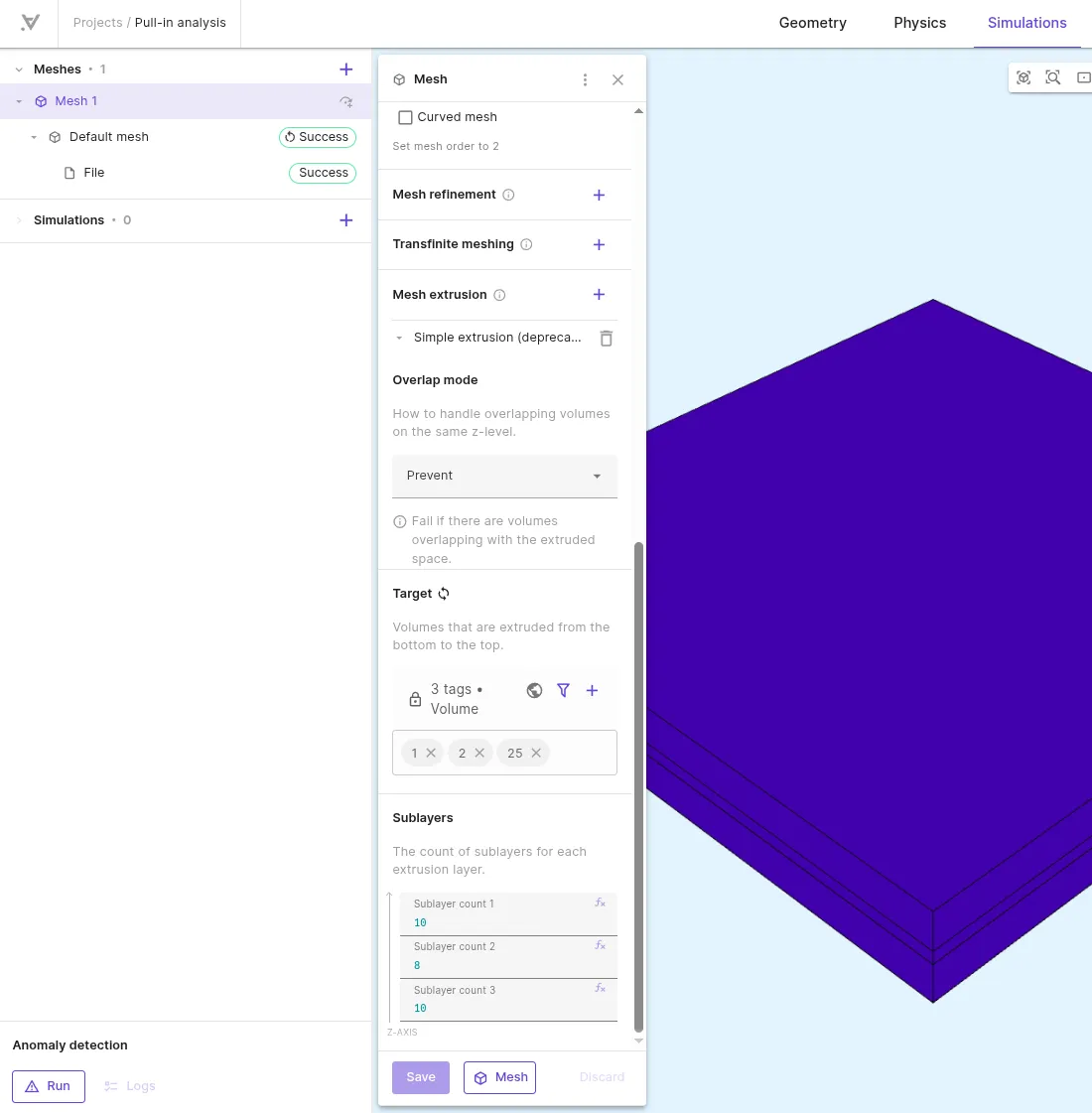
6. Add Mesh extrusion:

   Mesh entity	Overlap mode	Target	Sublayer counts
   Mesh extrusion	Prevent	All volumes 1, 2, 25	10
   			8
   			10

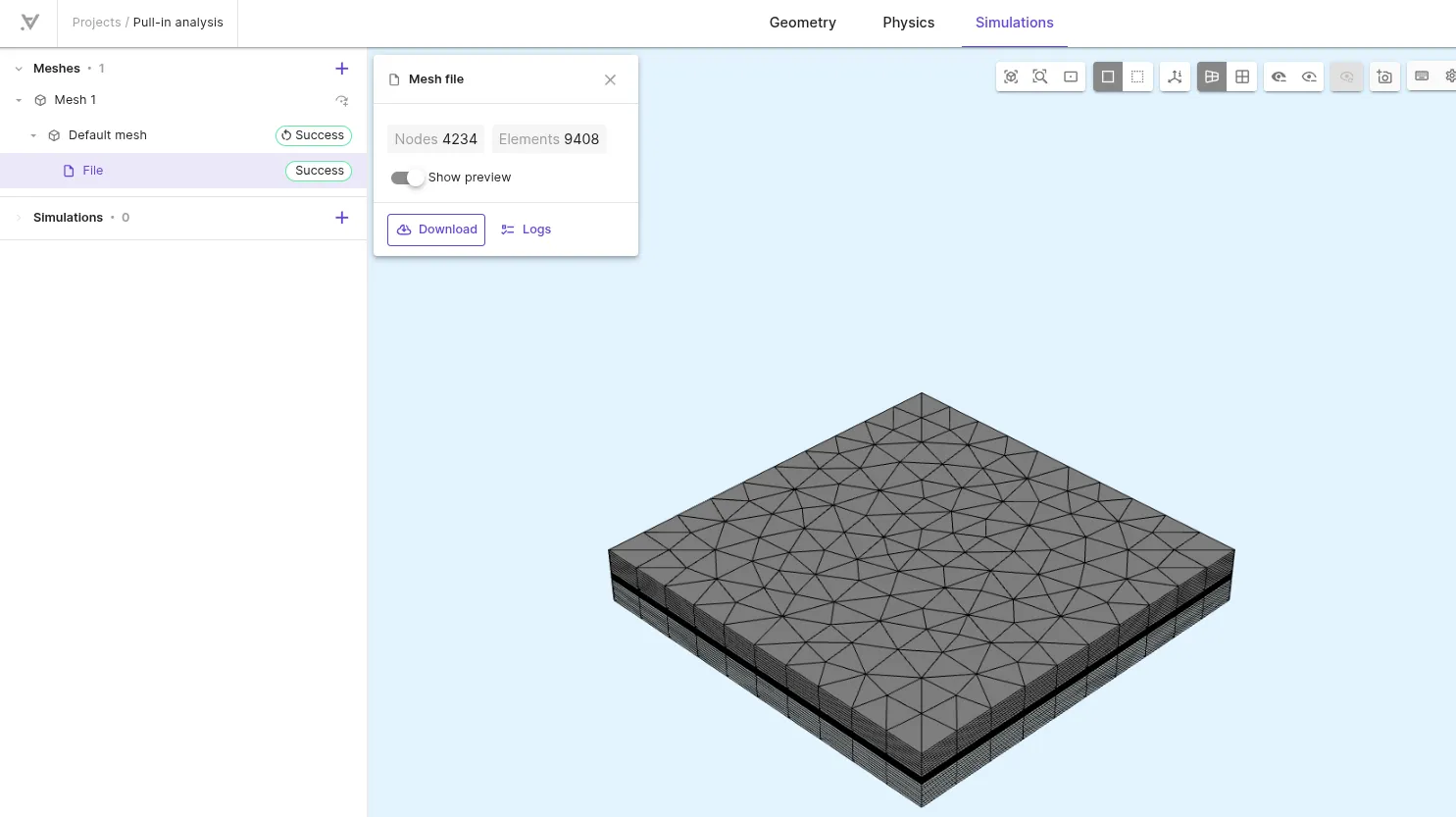
7. Run meshing and check the preview.

Step 5 - Apply settings and run the simulation

1. Add a new simulation.

2. Set Analysis Type to Steady state.

3. Select the mesh you created in Step 4 as the mesh for your simulation.

4. Add a Vdc sweep input with override expression linspace(5, 365, 73).

5. Add a custom value output and name it as max displacement in um. Set Output expression to maxvalue(reg.silicon_dioxide_target, -compz(u), 5) * 1e6.

6. The Solid mechanics physics considers geometric nonlinearity due to the Large displacement interaction. It is sufficient to consider geometric linearity for this simulation. To make this change, open the script and toggle on Scripting mode.

7. Scroll down to # Solid mechanics in the script, and replace the formulation with the line below:

   form += qs.integral(reg.silicon_dioxide_target, qs.predefinedelasticity(qs.dof(fld.u), qs.tf(fld.u), par.H()))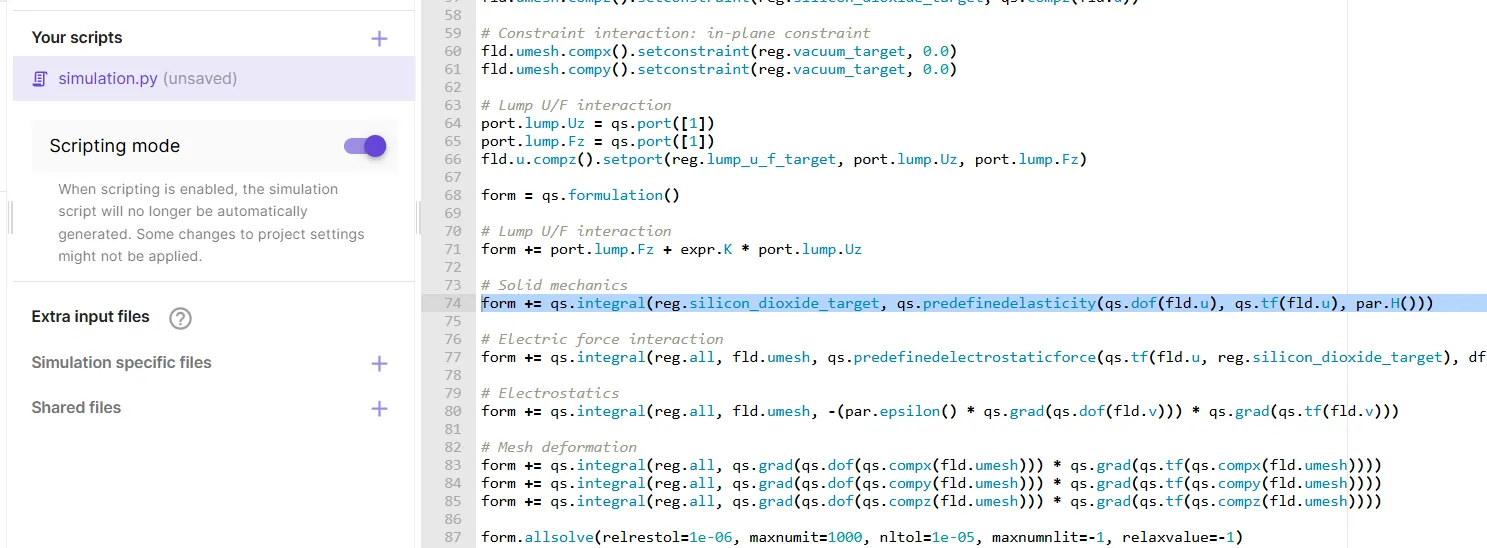

   

Your settings are now applied, and you can run the simulation.

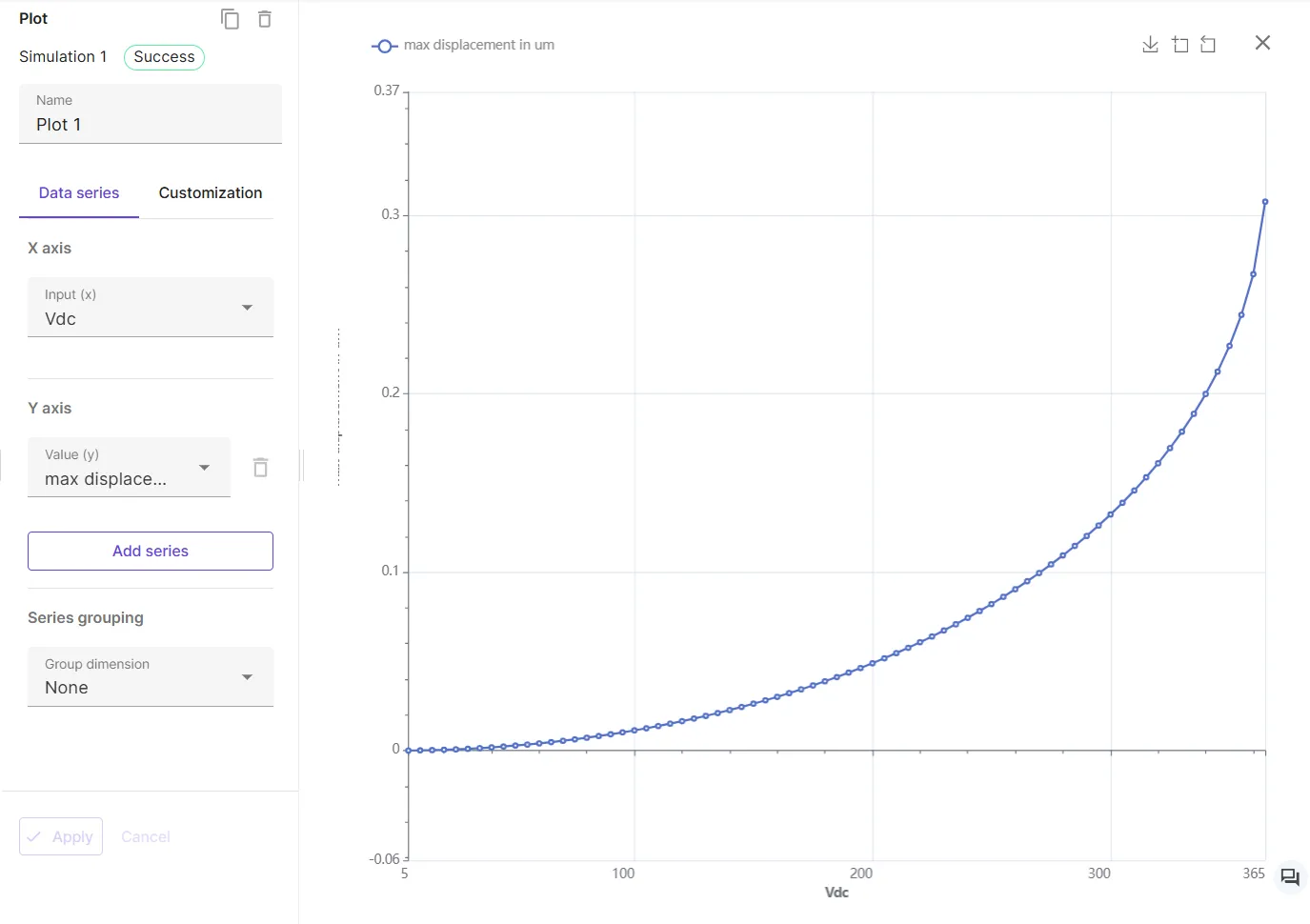
Step 5 - Plot results

Add a plot with Vdc in the X axis, and max displacement in um in the Y axis.

Tip: Plot results in real-time

To plot results, it is not necessary to wait until the whole sweep has finished.

A plot can be added once the first sweep job is finished, after which the plot will update automatically as the simulation progresses. Check the Logs to see when the first sweep job has finished before adding a plot.

References

Footnotes

1. Kaajakari, V. MEMS Tutorial: Pull-in voltage in electrostatic microactuators, 1-2. https://www.kaajakari.net/~ville/research/tutorials/pull_in_tutorial.pdf ↩